Теоремы о полноте.

 

 

Теорема 1: Во всяком исчислении предикатов первого порядка всякая теорема является логически общезначимой.

Доказательство: Так как частный случай тавтологии есть тавтология, то аксиомы, задаваемые схемами (А1) - (А3), логически общезначимы.

Пусть 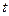- терм, свободный для переменной 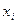в формуле 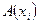. Тогда, если в произвольной интерпретации выполнена формула 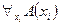, то выполнена и формула 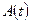. Поэтому формула истинна в любой интерпретации.

Если формула 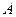не содержит переменной 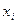в качестве свободной, то формула 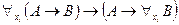истинна во всякой интерпретации. Следовательно, логически общезначимыми будут формулы, порождённые схемами (А4) - (А5). Правила вывода и сохраняют свойства логической общезначимости. Таким образом, всякая теорема любого исчисления предикатов логически общезначима.

Доказанная теорема – это только половина той теоремы о полноте, которую нужно доказать. Докажем предварительно несколько вспомогательных утверждений.

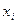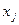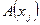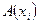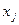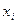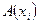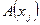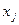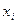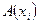Определение 1: Пусть переменные и различны и формула получается из формулы подстановкой переменной вместо всех свободных вхождений переменной , тогда формулы и называются подобными, если свободна для переменной в и 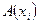не имеет свободных вхождений .

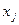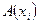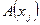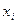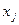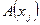Если и - подобны, то свободна для в и 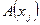не имеет свободных вхождений .

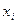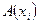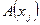Таким образом, подобие оказывается симметричным отношением. Иначе говоря, и подобны тогда и только тогда, когда 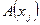имеет свободные вхождения 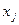в точности в тех местах, в которых 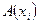имеет свободные вхождения переменной .

 

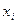Лемма 1: Если формулы 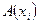и 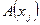подобны, то ├.

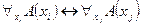Доказательство: по схеме аксиом (А4): ├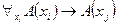. Применим правило обобщения (), тогда: ├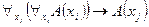и по схеме аксиом (А5) получим: ├.

Аналогично доказывается, что ├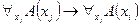. Применяя тавтологию 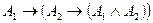и теорему 1 §9, получим: ├.

 

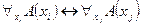Лемма 2: Если замкнутая формула 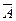теории невыводима в , то теория 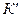, полученная из теории добавлением формулы 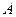в качестве аксиомы, является непротиворечивой.

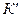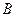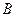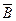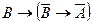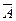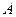Доказательство: Допустим, что теория противоречива. Это значит, что имеется формула , для которой ├К'и ├К'. Так как частным случаем тавтологии есть терема (теорема 1), то ├К'. Следовательно, ├К'и ├К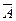. Поскольку формула 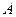замкнута, то по следствию 2 из теоремы дедукции имеем: ├К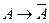. С другой стороны, по теореме 1 из §8 имеем: ├К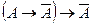. Поэтому ├К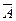, что противоречит условию. Противоречие возникло из неверного допущения.

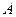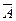Замечание: Подобным образом можно показать, что если формула невывоводима в , то добавление к теории формулы в качестве новой аксиомы не приводит к противоречию.

 

Лемма 3: Множество всех выражений всякой теории первого порядка счётно.

Значит, в частности, будут счётными множество всех термов, множество всех формул, множество всех замкнутых формул.

Доказательство: Каждому символу алфавита поставим в соответствие нечетное число по следующему правилу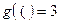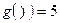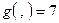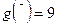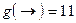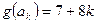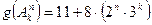: , , ,, , , , , . Выражению 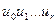поставим в соответствие число 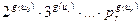, где - -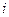е простое число. Видно, что при такой нумерации разные выражения получают разные номера. И можно пересчитать все выражения в порядке возрастания отнесённых им чисел.

Кроме того, можно не только эффективно распознавать символы теории , но оказывается возможным по любому числу узнавать, является ли оно в этой нумерации номером какого-нибудь выражения теории или нет. Сказанное верно для термов, формул, замкнутых формул и т. д. Если теория является к тому же эффективно аксиоматизируемой (т. е. имеется эффективная процедура, позволяющая для данной формулы решать вопрос о том, является ли она аксиомой), то можно перенумеровать все теоремы теории следующим образом: начнем с первой аксиомы в нумерации аксиом теории , добавив к ней все её непосредственные следствия по правилам и , применённым только к переменной ; затем добавим к полученному списку вторую аксиому (если её ещё там нет) и все непосредственные следствия формул этого расширенного за счет второй аксиомы списка с применением правила на этот раз уже по двум переменным и 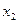. Если, поступая подобным образом, мы на 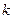- м шаге добавим к полученному списку формул 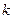- ю аксиому и ограничим действие правила переменными 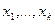, то при этом в конечном счете получим все теоремы теории. Так как всем этим теоремам будет присвоен некоторый номер (натуральное число), то множество всех теорем теории будет счётным. Что и требовалось доказать.

Однако, в отличие от случая выражений, формул, термов и т. д. оказывается, что существуют такие теории , для которых по любой наперёд заданной формуле нельзя сказать, встретится ли, в конце концов, эта формула в списке теорем.

Определение 2: Теория первого порядка называется полной, если для любой замкнутой формулы 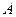из этой теории – либо ├К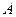, либо ├К.

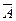Определение 3: Теория 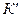первого порядка, имеющая те же символы, что и теория , называется расширением теории , если всякая теорема теории является также теоремой теории .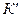

Для того, чтобы доказать, что теория 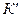является расширением теории , достаточно показать, что все собственные аксиомы теории являются теоремами теории .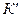

 

Лемма 4: (лемма Линденбауна).

Если теория первого порядка непротиворечива, то существует непротиворечивое полное её расширение.

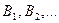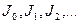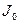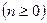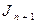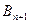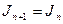Доказательство: Пусть - какой-нибудь пересчет всех замкнутых формул теории . Определим последовательность теорий следующим образом. Пусть есть , причём теория является непротиворечивой (по условию). Предположим, что теория определена, . Если неверно, что ├, то определим как теорию, полученную добавлением к теории в качестве новой аксиомы. Если же выполняется: ├, то полагаем, что . Пусть 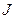есть теория первого порядка, получаемая, если в качестве аксиом взять все аксиомы всех теорий 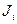. 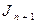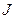Очевидно, что является расширением теории , а является расширением каждой из теорий , в том числе и теории 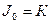. Для доказательства непротиворечивости теории 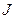достаточно доказать непротиворечивость каждой из теорий , так как всякий вывод противоречия в 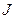использует лишь конечное число аксиом и, следовательно, является выводом противоречия в некоторой теории .

Докажем непротиворечивость теорий 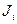индукцией по номеру 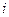. По условию, теория 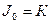непротиворечива. Допустим, что теория 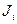непротиворечива. Тогда, если 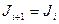, то и теория 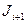непротиворечива. Если же 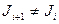, то, согласно определению 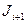, формула невыводима в 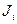, значит теория 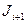непротиворечива (по лемме 2). Итак, непротиворечивость 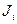влечёт непротиворечивость 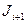. Тем самым доказано, что все теории 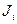непротиворечивы. Следовательно, непротиворечивой будет и теория .

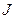Для доказательства полноты теории 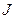рассмотрим произвольную замкнутую формулу 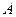теории . Очевидно, что 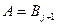при некотором 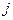(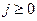). По определению теории 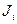имеем: либо ├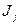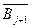, либо ├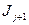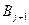, так как, если ├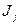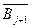, то 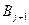объявляется аксиомой в 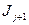. Следовательно, имеем: ├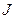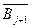или ├.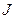

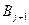Таким образом, теория 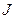является непротиворечивым полным расширением теории .

Замечание: Даже если мы умеем эффективно распознавать аксиомы теории , может, тем не менее, не существовать никакого эффективного способа распознавать (или даже перечислять) аксиомы теории 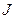, т. е. 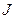может не быть эффективно аксиоматизированной теорией, даже если является таковой. Причиной этого может быть невозможность эффективного способа узнавать, выводима ли формула в (для любого ).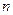

 

Теорема 2: Всякая непротиворечивая теория первого порядка имеет счётную модель (т. е. модель со счётной областью интерпретации).

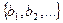Доказательство: Добавим к символам теории счётное множество новых предметных констант. Полученную таким образом новую теорию назовём теорией 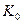. Её аксиомами являются все аксиомы теории , а также все частные случаи схем логических аксиом, содержащие новые предметные константы. Теория 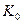непротиворечива. В самом деле, допустим, что для некоторой формулы 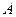существует вывод в 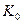формулы 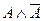. Заменим в этом выводе каждую предметную константу 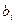другой предметной переменной, которая в этом выводе отсутствует. При такой замене все аксиомы этого вывода останутся аксиомами, и сохранится свойство формул быть непосредственным следствием предыдущих формул по правилам вывода. Таким образом, после этой замены снова будет получен вывод. Но теперь это будет вывод в , поскольку ни одна из формул не содержит предметных констант 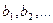. Последняя формула этого вывода тоже является противоречием, что противоречит условию непротиворечивости теории . Итак, теория 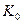непротиворечива.

Пусть 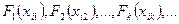- какой-нибудь пересчёт всех формул теории 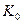, причём эти формулы содержат не более одной свободной переменной (лемма 4). Здесь 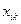- свободная переменная формулы 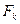. Если на самом деле формула 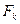не содержит свободной переменной, то 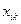есть . Выберем какую-нибудь последовательность , составленную из элементов множества 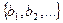таким образом, чтобы постоянная 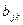не содержалась в 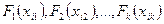и была отлична от .

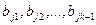Рассмотрим формулу: .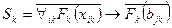

Определим теорию как теорию первого порядка, полученную из теории 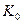в результате присоединения к аксиомам к ней формул 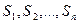в качестве новых аксиом. Теорию 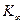определим, как теорию, полученную аналогичным образом: присоединением всех формул 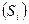к аксиомам теории 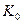. Всякий вывод в теории 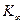содержит лишь конечное множество формул 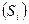, а значит, также является выводом и в некоторой теории . Следовательно, если все теории непротиворечивы, то непротиворечивой будет и теория .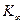

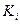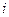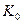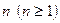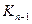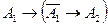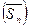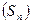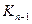
Методом математической индукции докажем непротиворечивость теории (индукцией по ). Непротиворечивость уже доказана. Допустим, что при некотором значении теория непротиворечива, а теория противоречива. Тогда, в силу тавтологии и теоремы 1, заключаем, что в выводима любая формула. В частности, ├. Поэтому ├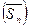. Так как формула 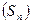замкнута, то по следствию 2 из теоремы дедукции имеем: ├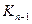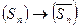. Теперь, принимая во внимание тавтологию и теорему 1, получаем: ├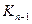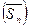, т. е. ├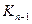. 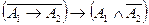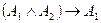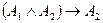Используя тавтологии , , и 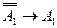, получаем: ├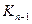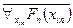и ├.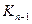

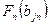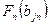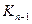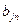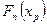Рассмотрим какой-нибудь вывод формулы в теории . Пусть - переменная, которая в этом выводе не встречается. Тогда, если в этом выводе всюду заменить на , то получим вывод в 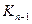, т. е. ├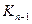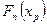. Далее, по правилу , имеем: ├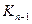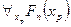. И, наконец, по лемме 1 имеем: ├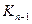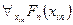. Здесь был использован тот факт, что формулы 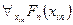и 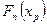подобны. С другой стороны, было установлено, что ├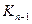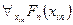. Таким образом, получено противоречие с предположением о непротиворечивости 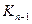. Поэтому теория также должна быть непротиворечивой. Итак, доказано, что все теории 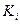, а сними вместе и теория 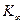, непротиворечивы.

Заметим, что 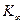есть непротиворечивое расширение теории 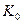. По лемме Линденбауна, 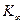имеет некоторое непротиворечивое полное расширение .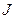