Формальная арифметика. Система аксиом.
Пусть  - теория первого порядка, в число предикатных букв которой входит
- теория первого порядка, в число предикатных букв которой входит  . Будем сокращенно писать
. Будем сокращенно писать  вместо
вместо 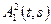 ; и
; и 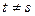 вместо
вместо  .
.
Определение 1: Теория  называется теорией первого порядка с равенством, если следующие формулы являются теоремами теории
называется теорией первого порядка с равенством, если следующие формулы являются теоремами теории  :
:
1) 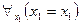 - рефлексивность равенства,
- рефлексивность равенства,
2)  - подстановочность равенства, где
- подстановочность равенства, где 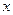 и
и  - предметные переменные,
- предметные переменные, 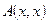 - произвольная формула, а
- произвольная формула, а  получается из
получается из 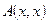 заменой каких-нибудь (не обязательно всех) свободных вхождений
заменой каких-нибудь (не обязательно всех) свободных вхождений 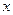 буквой
буквой  .
.
Можно доказать, что для любого терма 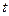 в теории с равенством выводима формула
в теории с равенством выводима формула 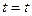 , а также свойства симметричности и транзитивности равенства.
, а также свойства симметричности и транзитивности равенства.
Арифметика, наряду с геометрией, является интуитивной областью математики. Поэтому будет естественным начинать процесс формализации и строгого обоснования математики именно с арифметики. Первое полуаксиоматическое построение арифметики было предложено Дедекиндом в 1901 году. Оно известно под названием «система аксиом Пеано». Эту систему можно сформулировать следующим образом:
(Р1) Число 0 – натуральное число.
(Р2) Для любого натурального числа 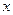 существует число
существует число 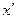 , непосредственно следующее за
, непосредственно следующее за 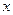 .
.
(Р3) 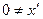 для любого натурального числа
для любого натурального числа 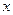 .
.
(Р4) Если  , то
, то 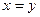 .
.
(Р5) Пусть 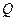 есть свойство, которым обладают одни натуральные числа, и которым могут не обладать другие числа. Если 1) натуральное число 0 обладает свойством
есть свойство, которым обладают одни натуральные числа, и которым могут не обладать другие числа. Если 1) натуральное число 0 обладает свойством 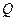 ; 2) для всякого натурального числа
; 2) для всякого натурального числа 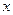 , обладающего свойством
, обладающего свойством 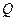 , число
, число 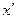 также обладает свойством
также обладает свойством 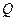 ; тогда свойством
; тогда свойством 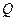 обладают все натуральные числа (принцип индукции).
обладают все натуральные числа (принцип индукции).
Этих аксиом, вместе с некоторым фрагментом теории множеств, достаточно для построения не только арифметики, но и теории рациональных, вещественных и комплексных чисел (это было сделано немецким математиком Ландау в 1930 году). Однако в этих аксиомах содержатся интуитивные понятия, такие, например, как «свойство». Это мешает всей системе быть строгой формализацией. Поэтому далее будет построена теория первого порядка 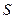 , основанная на системе аксиом Пеано, которая окажется достаточной для вывода всех основных результатов элементарной арифметики. Эта теория первого порядка будет иметь единственную предикатную букву
, основанная на системе аксиом Пеано, которая окажется достаточной для вывода всех основных результатов элементарной арифметики. Эта теория первого порядка будет иметь единственную предикатную букву  , единственную предметную константу
, единственную предметную константу  и три функциональные буквы
и три функциональные буквы  . Впрочем, чтобы не порывать с привычными по неформальной арифметике обозначениями, в дальнейшем мы будем писать
. Впрочем, чтобы не порывать с привычными по неформальной арифметике обозначениями, в дальнейшем мы будем писать  вместо
вместо 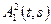 ,
,  вместо
вместо  и
и  вместо, соответственно,
вместо, соответственно, 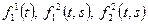 , где
, где 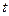 и
и 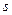 - термы.
- термы.
Собственные аксиомы теории S:
(S1)  ;
;
(S2)  ;
;
(S3) 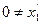 ;
;
(S4) 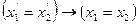 ;
;
(S5) 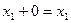 ;
;
(S6)  ;
;
(S7) 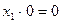 ;
;
(S8) 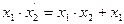 ;
;
(S9)  , где
, где  - произвольная формула теории
- произвольная формула теории 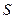 .
.
Замечание 1: Если натуральное число, которое не следует ни за каким другим натуральным числом, называть ни нулём, а единицей (обозначать: 1), то аксиомы (S3), (S5) и (S7) необходимо заменить соответственно на следующие аксиомы:
(S3*)  (число 1 не следует ни за каким другим натуральным числом);
(число 1 не следует ни за каким другим натуральным числом);
(S5*)  ;
;
(S7*) 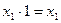 .
.
А также в аксиоме (S9) следует заменить  на
на 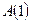 .
.
Замечание 2: Аксиомы (S1) – (S8) являются конкретными формулами, в то время как (S9) представляет собой схему аксиом, т. к. формула  - произвольная. При этом схема аксиом (S9), которую будем называть принципом математической индукции, не соответствует полностью аксиоме (Р5) системы аксиом Пеано. Это происходит потому, что в аксиоме Пеано интуитивно предполагается, что число различных свойств натуральных чисел несчетно (т. е. имеет мощность
- произвольная. При этом схема аксиом (S9), которую будем называть принципом математической индукции, не соответствует полностью аксиоме (Р5) системы аксиом Пеано. Это происходит потому, что в аксиоме Пеано интуитивно предполагается, что число различных свойств натуральных чисел несчетно (т. е. имеет мощность  ), а схема аксиом (S9) счётна, множество всех формул
), а схема аксиом (S9) счётна, множество всех формул  теории
теории 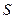 счётно.
счётно.
Замечание 3: Аксиомы (S3) и (S4) соответствуют аксиомам (Р3) и (Р4) системы аксиом Пеано. Аксиомы (Р1) и (Р2) системы Пеано обеспечивают существование  и операции «непосредственно следующий», которым в теории
и операции «непосредственно следующий», которым в теории 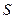 соответствует предметная константа
соответствует предметная константа  и функциональная буква
и функциональная буква 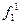 . Аксиомы (S1) и (S2) обеспечивают необходимые свойства равенства, которые Дедекиндом и Пеано предполагались интуитивно очевидными. Аксиомы (S5) - (S8) представляют собой рекурсивные равенства, служащие определением операций сложения и умножения.
. Аксиомы (S1) и (S2) обеспечивают необходимые свойства равенства, которые Дедекиндом и Пеано предполагались интуитивно очевидными. Аксиомы (S5) - (S8) представляют собой рекурсивные равенства, служащие определением операций сложения и умножения.
С помощью правила modus ponens и схемы аксиом (S9) можно получить правило индукции: из  и
и  выводимо
выводимо 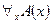 .
.
Следующая лемма является очевидным и непосредственным следствием аксиом.
Лемма 1: Для любых термов  ,
, 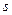 и
и 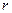 теории
теории 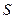 следующие формулы являются теоремами в
следующие формулы являются теоремами в 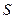 :
:
(S1*) 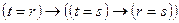 ;
;
(S2*) 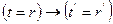 ;
;
(S3*)  ;
;
(S4*) 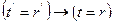 ;
;
(S5*)  ;
;
(S6*) 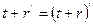 ;
;
(S7*)  ;
;
(S8*)  .
.
Доказательство: Все свойства (S1*) – (S8*) доказываются одинаково. Сначала необходимо образовать замыкание для аксиом (S1) - (S8) по правилу обобщения ( ), а затем применить аксиому (А4) (логическая аксиома логики предикатов:
), а затем применить аксиому (А4) (логическая аксиома логики предикатов:  , где
, где 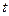 - терм, свободный для
- терм, свободный для 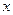 в
в  с подходящими термами
с подходящими термами 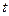 ,
, 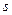 ,
, 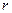 ).
).
Далее будут рассмотрены обычные свойства равенства (для теории 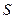 первого порядка с равенством).
первого порядка с равенством).
Теорема 1: Для любых формул  ,
, 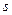 и
и 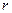 теории
теории 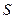 следующие свойства являются теоремами этой теории.
следующие свойства являются теоремами этой теории.
(a) 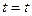 ;
;
(b) 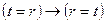 ;
;
(с) 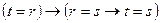 ;
;
(d) 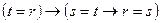 ;
;
(е)  ;
;
(f) 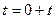 ;
;
(g) 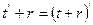 ;
;
(h) 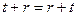 ;
;
(i)  ;
;
(j)  ;
;
(l)  ;
;
(m) 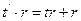 ;
;
(n) 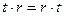 ;
;
(о) 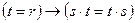 .
.
Доказательство: Докажем некоторые свойства для примера.
(a) 1.  (по аксиоме (S5*));
(по аксиоме (S5*));
2.  (по аксиоме (S1*));
(по аксиоме (S1*));
3.  (из пунктов 1 и 2 по правилу
(из пунктов 1 и 2 по правилу  );
);
4. 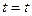 (из пунктов 1 и 3 по правилу
(из пунктов 1 и 3 по правилу  ).
).
(d) 1. 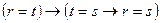 (свойство (с));
(свойство (с));
2. 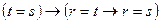 (1, тавтология);
(1, тавтология);
3. 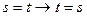 (свойство (b));
(свойство (b));
4. 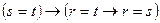 (из 2,3, тавтология);
(из 2,3, тавтология);
5.  (4, тавтология).
(4, тавтология).
(е) Применим правило индукции к формуле:  .
.
Остальные свойства можно доказать аналогично.
Теорема 2: Для любых термов  ,
, 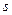 и
и 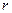 следующие формулы являются теоремами теории
следующие формулы являются теоремами теории 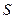 :
:
(a)  (дистрибутивность слева);
(дистрибутивность слева);
(b)  (дистрибутивность слева);
(дистрибутивность слева);
(с)  (ассоциативность умножения);
(ассоциативность умножения);
(d)  .
.
Доказательство:
(a) Доказательство можно провести индукцией по  ├
├  .
.
(b) Следует из пункта (a) и коммутативности умножения (см. теорему 1, пункт (n)).
(с) Можно доказать индукцией по z: ├  .
.
(d) Доказывается индукцией по z с использованием аксиомы (S4*). Можно показать, что ├  .
.
В дальнейшем термы 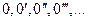 мы будем называть цифрами, и обозначать, как обычно, 0, 1, 2, 3, ... . Для любого неотрицательного
мы будем называть цифрами, и обозначать, как обычно, 0, 1, 2, 3, ... . Для любого неотрицательного 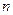 соответствующая цифра – это 0 с
соответствующая цифра – это 0 с 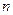 штрихами.
штрихами.
Натуральные числа можно определить рекурсивно: 0 – есть число; если 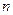 - натуральное число, то и
- натуральное число, то и 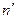 также натуральное число.
также натуральное число.
Теорема 3:
(a) ├  ;
;
(b) ├  ;
;
(с) ├ 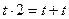 ; (и т. д. для 3, 4, ...);
; (и т. д. для 3, 4, ...);
(d) ├  ;
;
(е) ├ 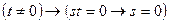 ;
;
(f) ├ 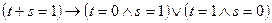 ;
;
(g) ├ 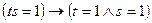 ;
;
(h) ├ 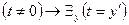 ;
;
(i) ├  ;
;
(j) ├ 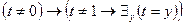 .
.
Доказательство:
(a) 1. 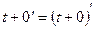 (S6*);
(S6*);
2.  (S5*);
(S5*);
3. 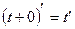 (S2*);
(S2*);
4. 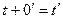 (1, 3, теорема 1);
(1, 3, теорема 1);
5.  (4, определение цифры
(4, определение цифры 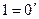 ).
).
(с) 1. 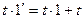 (S8*);
(S8*);
2.  (b);
(b);
3. 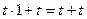 (2, теорема 1, (е));
(2, теорема 1, (е));
4.  (1, 3, теорема 1, (с));
(1, 3, теорема 1, (с));
5. 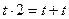 (4, определение цифры 2).
(4, определение цифры 2).
(d) Обозначим через  формулу
формулу  . Тогда видно, что ├
. Тогда видно, что ├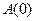 . Из аксиомы (S3*) ├
. Из аксиомы (S3*) ├ 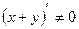 . Отсюда на основании аксиомы (S6*) получаем: ├
. Отсюда на основании аксиомы (S6*) получаем: ├  . Следовательно, в силу тавтологии
. Следовательно, в силу тавтологии 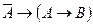 , имеем: ├
, имеем: ├ 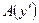 . Далее, в силу тавтологии
. Далее, в силу тавтологии  , получаем: ├
, получаем: ├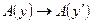 . Применяя правило индукции, имеем: ├
. Применяя правило индукции, имеем: ├ 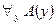 . Затем, с помощью правил обобщения и логической аксиомы (А4), получаем требуемое утверждение (d).
. Затем, с помощью правил обобщения и логической аксиомы (А4), получаем требуемое утверждение (d).
Остальные свойства доказываются аналогично.
Определение 2: а)  означает, что
означает, что 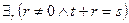 ;
;
б) 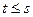 означает, что
означает, что 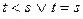 ;
;
в)  означает, что
означает, что  ;
;
г)  означает, что
означает, что  ;
;
д) 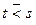 означает, что
означает, что  .
.
Теорема 4: Каковы бы ни были термы  ,
, 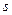 и
и 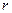 , следующие формулы выводимы в теории
, следующие формулы выводимы в теории 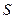 :
:
(a) 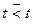 ;
;
(b) 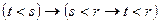 ;
;
(с) 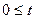 ;
;
(d)  ;
;
(е) 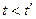 .
.
Доказательство:
(a) Следует из того, что  . Индукцией по z можно доказать, что ├
. Индукцией по z можно доказать, что ├  .
.
(b) - (е) предлагается доказать самостоятельно.
Определение 3: Будем говорить, что 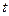 делится на
делится на 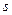
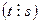 , если существует
, если существует 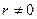 такое, что
такое, что  .
.
Теорема 5: Следующие формулы выводимы в теории 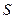 :
:
(a)  ;
;
(b)  ;
;
(с) 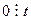 ;
;
(d)  ;
;
(е) 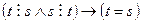 ;
;
(f)  .
.
Доказательство: (a), (b):  .
.
Аналогично доказываются остальные свойства делимости.
Теорема 6: (Полная индукция).
Пусть свойство 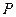 таково, что для любого натурального числа
таково, что для любого натурального числа 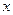 , из того, что этим свойством обладают все натуральные числа, меньшие
, из того, что этим свойством обладают все натуральные числа, меньшие 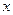 , вытекает, что им обладает и число
, вытекает, что им обладает и число 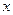 . Тогда свойством
. Тогда свойством 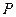 обладают все натуральные числа, т. е.: ├
обладают все натуральные числа, т. е.: ├ 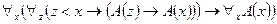 .
.
Доказательство: По условию, свойством 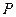 обладают все натуральные числа, меньшие
обладают все натуральные числа, меньшие 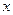 . Значит, в частности, свойством
. Значит, в частности, свойством 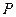 обладает и число 0, и число, за которым следует
обладает и число 0, и число, за которым следует 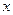 . Следовательно, по аксиоме индукции, выполнено
. Следовательно, по аксиоме индукции, выполнено 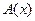 . По правилу обобщения (аксиома (А4),
. По правилу обобщения (аксиома (А4),  ) имеем:
) имеем: 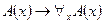 . Что и требовалось доказать.
. Что и требовалось доказать.
Далее можно определить и изучать арифметические функции и отношения. Например, вычислимые функции, т. е. функции, получаемые из простейших 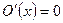 ,
, 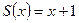 и
и 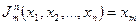 , где
, где 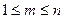 , с помощью операторов подстановки, примитивной рекурсии и минимизации. Эти вопросы относятся к разделу теории алгоритмов.
, с помощью операторов подстановки, примитивной рекурсии и минимизации. Эти вопросы относятся к разделу теории алгоритмов.