Линейные функции. Монотонные функции.
Рассмотрим систему функций:
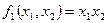 ,
,  ,
, 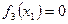 ,
, 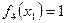 . (***)
. (***)
Суперпозицию функций системы (***) можно преобразовать, пользуясь правилами элементарной алгебры и специальными правилами:
 ,
, 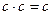 ,
, 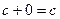 .
.
В частности, если раскрыть скобки и привести подобные члены, то полученная сумма «одночленов» называется многочленом Жегалкина.
Теорема 1: Для любой функции алгебры логики существует многочлен Жегалкина, задающий эту функцию.
Доказательство: Действительно, в предыдущем параграфе было доказано, что система функций 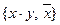 является полной в
является полной в  . Полную систему образует и система функции
. Полную систему образует и система функции 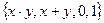 , так как
, так как 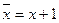 . Теорема доказана.
. Теорема доказана.
Можно доказать, что каждая функция 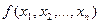 представляется в виде многочлена Жегалкина единственным образом. Это следует из доказанной теоремы и того факта, что число многочленов Жегалкина от переменных
представляется в виде многочлена Жегалкина единственным образом. Это следует из доказанной теоремы и того факта, что число многочленов Жегалкина от переменных 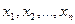 равно
равно 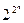 , т. е. совпадает с числом всех функций алгебры логики от этих переменных.
, т. е. совпадает с числом всех функций алгебры логики от этих переменных.
Определение 1: Функция 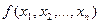 называется линейной, если имеет место соотношение:
называется линейной, если имеет место соотношение: 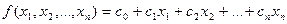 .
.
Теорема 2: Функция, представленная многочленом Жегалкина, существенно зависит от всех входящих в него переменных.
Доказательство: Пусть, например,  – переменная, о которой идёт речь в условии теоремы. Сгруппируем члены, и вынесем
– переменная, о которой идёт речь в условии теоремы. Сгруппируем члены, и вынесем  за скобки. Получим:
за скобки. Получим:
 ,
,
где функция 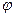 – не равна тождественно нулю. В противном случае (в силу единственности представления функции многочленом Жегалкина)
– не равна тождественно нулю. В противном случае (в силу единственности представления функции многочленом Жегалкина)  не входила бы в многочлен для
не входила бы в многочлен для 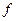 . Возьмем значения переменных
. Возьмем значения переменных 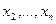 , на которых
, на которых 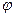 равна
равна 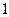 . Тогда значение
. Тогда значение 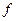 будет зависеть от значения
будет зависеть от значения  .
.
Замечание: Множество всех линейных функций составляет замкнутый класс.
Для того чтобы произвольную функцию представить многочленом Жегалкина, нужно выразить все операции через конъюнкцию и отрицание, учитывая, что 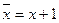 . Затем следует привести подобные слагаемые, используя при этом правила, указанные выше:
. Затем следует привести подобные слагаемые, используя при этом правила, указанные выше:  ,
, 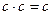 ,
, 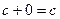 .
.
Далее будет рассмотрен класс функций, обладающих несколько иными свойствами.
Упорядочим множество  , полагая
, полагая 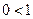 . Поскольку мы будем иметь дело с функциями от нескольких переменных, то введем частичное упорядочение двоичных наборов одинаковой длины.
. Поскольку мы будем иметь дело с функциями от нескольких переменных, то введем частичное упорядочение двоичных наборов одинаковой длины.
Определение 2: Пусть  — двоичные наборы. Будем говорить, что
— двоичные наборы. Будем говорить, что 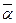 предшествует
предшествует 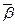 (обозначение
(обозначение 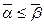 ), если
), если 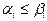 для всех
для всех 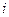 , причем, по крайней мере, для одного
, причем, по крайней мере, для одного 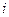 , имеет место строгое неравенство. Будем писать:
, имеет место строгое неравенство. Будем писать: 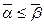 , если
, если 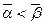 или наборы
или наборы 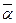 и
и 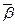 совпадают.
совпадают.
Это упорядочение является только частичным, так как не всякие наборы можно сравнивать.
Определение 3: Функция алгебры логики  называется монотонной, если для всяких наборов
называется монотонной, если для всяких наборов  таких, что
таких, что 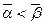 имеем неравенство:
имеем неравенство: 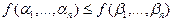 .
.
Например, нетрудно заметить, что константы, конъюнкция, дизъюнкция являются монотонными функциями.
Теорема 3: Множество всех монотонных функций образует замкнутый класс.
Доказательство: Т.к. функция 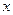 — монотонна, то достаточно показать, что если функции
— монотонна, то достаточно показать, что если функции 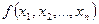 ,
, 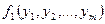 ,
, 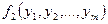 ,...,
,...,  являются монотонными, то функция монотонной будет также функция:
являются монотонными, то функция монотонной будет также функция:
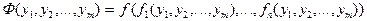 .
.
Рассмотрим два произвольных набора  таких, что
таких, что 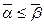 . В этом случае
. В этом случае 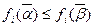 , где
, где 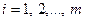 . Следовательно,
. Следовательно,
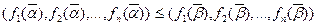
и, значит, в силу монотонности функции 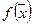 имеет место неравенство:
имеет место неравенство:  . Теорема доказана.
. Теорема доказана.