Теорема Поста.
В предыдущем параграфе были рассмотрены некоторые классы булевых функций. В каждый класс попадают функции, обладающие определённым свойством. Для удобства введём следующие обозначения:
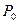 — класс булевых функций, сохраняющих 0;
— класс булевых функций, сохраняющих 0;
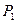 — класс функций, сохраняющих 1;
— класс функций, сохраняющих 1;
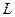 — класс линейных функций;
— класс линейных функций;
 — класс монотонных функций;
— класс монотонных функций;
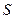 — класс самодвойственных функций.
— класс самодвойственных функций.
Все перечисленные классы функционально замкнуты. Теперь рассмотрим критерий полноты.
Теорема 1: (теорема Поста). Для полноты системы функций необходимо и достаточно, чтобы для каждого из классов 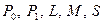 в системе
в системе 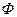 нашлась функция
нашлась функция  , ему не принадлежащая.
, ему не принадлежащая.
Доказательство теоремы было рассмотрено в курсе дискретной математики.
При проверке, выполняются ли для некоторой системы функций 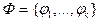 условия теоремы Поста, мы будем составлять таблицы, которые назовем таблицами Поста. Они будут иметь вид:
условия теоремы Поста, мы будем составлять таблицы, которые назовем таблицами Поста. Они будут иметь вид:
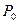
| 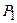
| 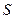
| 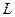
| 
| |

| |||||

| |||||
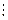
| |||||
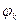
|
В клетках таблицы Поста ставится плюс или минус, в зависимости от того, входит функция, стоящая в данной строке, в класс, стоящий в данном столбце, или не входит. Для полноты системы функции необходимо и достаточно (в силу теоремы Поста), чтобы в каждом столбце присутствовал хотя бы один минус. Это будет означать, что для каждого из классов 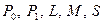 в данной системе функций есть функция, не принадлежащая этому классу. Например, таблица Поста для системы функций
в данной системе функций есть функция, не принадлежащая этому классу. Например, таблица Поста для системы функций 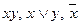 имеет вид:
имеет вид:
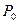
| 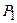
| 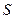
| 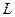
| 
| |
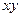
| + | + | - | - | + |
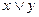
| + | + | - | - | + |
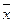
| - | - | + | + | - |
Данная система функций является полной, т. к. выполнены условия теоремы Поста. Кроме того, видно, что если убрать одну строку (например, последнюю), то получим неполную систему (знак плюс стоит в каждой строке в столбцах).
Из этой таблицы видно, что каждая из систем функций 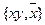 ,
,  составляют базис полной системы.
составляют базис полной системы.
Определение 1: Функционально замкнутые классы, отличные от пустого класса и от совокупности всех функций алгебры логики, называются собственными функционально замкнутыми классами.
Определение 2: Собственный функционально замкнутый класс называется предполным, если он не содержится ни в каком функционально замкнутом классе, отличном от самого себя и от класса всех функций алгебры логики.
Следствие (из теоремы Поста):
1. Система функций 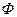 не полна тогда и только тогда, когда она целиком входит в один из классов
не полна тогда и только тогда, когда она целиком входит в один из классов 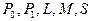 .
.
2. Ни один из классов 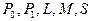 не содержится в другом.
не содержится в другом.
3. Действительно, если бы какой-либо класс содержался в другом, то в формулировке теоремы Поста этот класс можно было бы отбросить.
Всякий собственный функционально замкнутый класс содержится в одном из классов 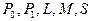 .
.
Действительно, если некоторый функционально замкнутый класс 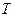 не содержится ни в одном из пяти указанных классов, то для каждого из них в классе
не содержится ни в одном из пяти указанных классов, то для каждого из них в классе 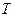 найдется функция, ему не принадлежащая. Но тогда по теореме Поста
найдется функция, ему не принадлежащая. Но тогда по теореме Поста 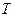 содержит все функции алгебры логики.
содержит все функции алгебры логики.
Теорема 2: Функционально замкнутые классы 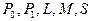 являются предполными, и других предполных классов нет.
являются предполными, и других предполных классов нет.
Доказательство: Из следствия 3 теоремы Поста следует, что других предполных классов нет, а из следствия 2 следует, что каждый из пяти перечисленных классов является предполным.
Замечание: Теорема Поста позволяет выяснить вопрос о том, является ли полная система базисом. Это удобно делать опять-таки с помощью таблиц Поста. Причем нетрудно видеть, что всякий базис не может содержать более пяти функций.
На самом деле имеет место более точный результат.
Теорема 3: Всякий базис полной системы функций не может содержать более четырех функций.
Доказательство: Заметим сначала, что если монотонная функция не сохраняет нуль, то она тождественно равна единице. Действительно, т. к. нулевой набор меньше любого другого, то из равенства на нем монотонной функции единице следует ее тождественное равенство единице (на остальных наборах значение функции не может быть меньше, чем на нулевом наборе). Аналогично, если монотонная функция не сохраняет единицу, то она тождественно равна нулю.
Возьмем теперь функцию, не сохраняющую нуль. В силу сделанного замечания, она или является немонотонной или является тождественной единице, т. е. несамодвойственной функцией. Итак, в полной системе обязательно найдется функция, не принадлежащая сразу двум предполным классам. Тогда к этой функции можно присоединить не более трех функций из рассматриваемой системы так, чтобы удовлетворялись условия теоремы Поста. Значит, в базисе не может быть более четырех функций. Что и требовалось доказать.