Формулы алгебры логики. Тавтологии.

В алгебре выводятся формулы, которые остаются верными, какие бы числа не подставляли вместо букв, входящих в эти формулы. Подобным образом в алгебре высказываний конструируются формулы из некоторых букв, вместо которых можно подставлять любые высказывания. Введём символы 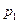, ,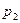..., которые будем называть пропозиционными переменным (или пропозиционными буквами).

Из пропозиционных букв, логических операций и скобок можно составлять различные выражения; некоторые из них называются формулами.

Определение 1: Формулами исчисления высказываний являются:

а) каждая пропозиционная буква;

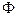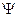б) если и - формулы, то формулами являются также , , , , , .

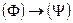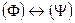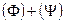Выражения, перечисленные в пункте б), называются соответственно отрицанием формулы 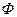, конъюнкцией, дизъюнкцией, импликацией, эквивалентностью, сложением по модулю 2 формул 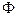и .

И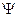з определения следует, что каждая формула исчисления высказываний либо является пропозиционной буквой, либо может быть получена из конечного числа пропозиционных букв путём многократного применения пункта б). Сначала к исходным пропозиционным буквам, затем к полученным формулам и т. д.

Для уменьшения числа скобок в формулах принято пропозиционные буквы и отрицание в скобки не заключать. Затем, как и в алгебре, принята приоритетность операций в такой последовательности: ¯, , , , .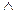

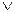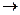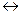Так, например, выражение 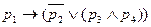является формулой, в которой все скобки можно опустить. А в выражении 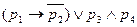скобки опускать нельзя.

Определение 2: Формулы исчисления высказываний, образованные из пропозиционных букв 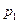, ,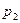..., , 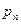логических операций и скобок, будем обозначать 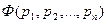. Если в этой формуле заменить пропозиционные буквы 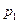, ,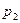..., 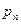соответственно высказываниями 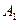, ,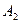..., , 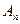то получим составное высказывание 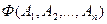, которое назовём логическим значением формулы при , ,..., .

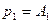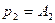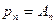Из определения следует, что значение формулы 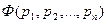для данных высказываний 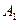, ,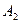..., 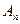зависит только от логического значения последних. Эту зависимость можно выразить с помощью таблицы из 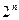строк. Число строк таблицы равно числу возможных комбинаций значений высказываний 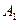, ,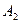..., . 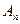В строках последнего столбца указываются соответствующие значения формулы. Например, для формулы 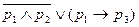таблица истинности имеет следующий вид:

 

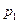
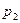
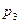
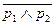
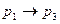
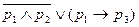
л	л	л	и	и	и
л	л	и	и	и	и
л	и	л	и	и	и
л	и	и	и	и	и
и	л	л	и	л	и
и	л	и	и	и	и
и	и	л	л	л	л
и	и	и	л	и	и

 

Здесь для облегчения заполнения таблицы в неё введены дополнительные столбцы, в которых указаны значения отдельных частей формулы.

Определение 3: Формула исчисления высказываний называется тавтологией (или тождественно истинной формулой), если её значения есть «истина» для всех наборов значений пропозиционных переменных, входящих в эту формулу.

Нахождение тавтологий – это основная задача логики высказываний, так как они выражают законы логического мышления.

Для произвольной формулы легко проверить, является ли она тавтологией. Для этого составляют таблицу истинности этой формулы, или проверяют с помощью рассуждений. Например, для рассмотренной формулы 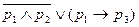можно выяснить, когда обе части дизъюнкци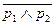и и 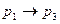будут ложными. Первая часть 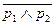ложна, когда 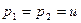. Вторая часть 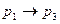принимает ложное значение, когда 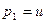, 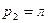. Таким образом, 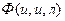, значит, формула не является тавтологией.

 

Теорема 1: Следующие формулы исчисления высказываний являются тавтологиями:

1) 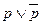- закон исключенного третьего;

2) - закон отрицания противоречия;

3) 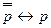- закон двойного отрицания;

4) ,

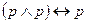5) ,

6) ,

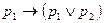7) 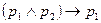- законы упрощения;

8) ,

9) 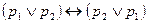- законы коммутативности конъюнкции и дизъюнкции;

10) ,

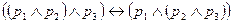11) 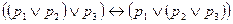- законы ассоциативности операци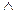й и ,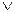

12) ,

13) - законы дистрибутивности,

14) ,

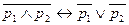15) 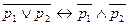- законы де Моргана;

16) 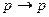- закон тождества;

17) 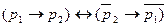- закон контрапозиции;

18) 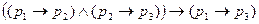- правило цепного заключения;

19) ,

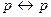20) ,

21) 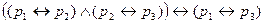- свойства рефлексивности, симметричности и транзитивности операции ↔ соответственно;

22) 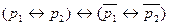- закон противоречия.

 

Доказательство: Эту теорему можно доказать, построив таблицу истинности для каждой тавтологии. При этом для любого набора значений пропозиционных переменных, входящих в формулу (т. е. для каждой строки таблицы), формула должна принимать значение «истина».

Докажем некоторые из перечисленных тавтологий.

(1) Действительно, по определению отрицания, для любого высказывания 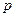, либо оно, либо его отрицание истинно. И, следовательно, дизъюнкция 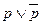истинна, т. к. одна из её компонент обязательно будет истинной. Первое утверждение теоремы доказано.

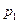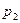(7) Пусть и – некоторые высказывания. Если конъюнкция 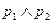истинна, то и высказывание 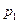истинно. Таким образом, для любых двух высказываний значение импликации 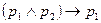не может быть ложью. Значит это тавтология.

(14) Пусть 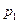и 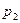– два высказывания. Рассмотрим два составных высказывания 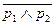и 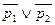. Допустим, что отрицание 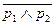истинно. Тогда конъюнкция 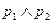будет ложна, а, следовательно, по крайней мере, одно из высказывани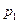й или 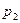ложно. Но тогда, по крайней мере, одно из высказывани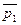й или 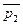– истинно, а, следовательно, их дизъюнкция 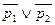тоже истинна.

Допустим далее, что отрицание 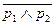ложно. Тогда конъюнкция 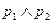истинна. Следовательно, оба высказывания 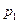и 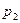истинны, а их отрицания 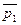, 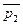– оба ложны, т. е. их дизъюнкция 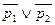ложна. Таким образом, для любых значений пропозиционных переменных, входящих в формулу (14), она всегда принимает значение «истина», а значит, является тавтологией.

Остальные утверждения теоремы доказываются аналогично.

Теорема 2: Если формулы 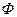и 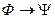- тавтологии, то 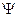– тавтология.

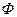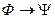Доказательство. Докажем от противного. Пусть и - тавтологии, а 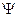- не тавтология. Это значит, что при некотором наборе значений пропозиционных переменных, входящих в данную формулу, 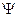принимает значение «ложь». Так как 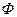– тавтология, то при этом же наборе значений пропозиционных букв она всегда принимает значение «истина». Но тогда формула 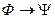будет ложной, а это противоречит тождественной истинности этой формулы. Значит, допущение о том, что 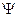может принимать значение «ложь» неверно. Следовательно, 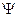всегда принимает значение «истина», т. е. является тавтологией. Теорема доказана.

Теорема 3: Пусть формула 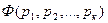есть тавтология, и формула получается заменой пропозиционных букв 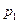, ,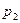..., 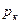формулами 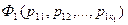, ,..., , 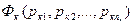тогда полученная формула есть тавтология, т. е. подстановка в тавтологию приводит к тавтологии.

Доказательство: Пусть 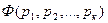есть тавтология и пусть задано произвольное распределение истинностных значений пропозиционных переменных 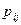, входящих в формулы 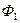, ,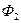..., . 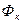Тогда формулы 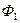, ,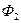..., 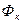примут некоторые истинностные значения , ,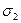..., 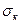(каждое 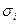есть или 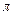). Тогда формула, полученная с помощью подстановки, примет значение 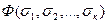. Но так как формула 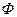есть тавтология, то это значение есть «истина». Значит, полученная после подстановки формула всегда принимает значение «истина». Теорема доказана.

Определение 4: Формула исчисления высказываний называется тождественно ложной (или противоречием), если при любом наборе значений пропозиционных переменных, входящих в эту формулу, она принимает значение «ложь».

Например, формулы 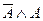, 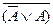при любом значении принимают значение «ложь», а значит являются тождественно ложными.

Определение 5: Формула исчисления высказываний называется выполнимой, если существует такой набор значений пропозиционных переменных, входящих в эту формулу, при котором формула принимает значение «истина».

Для того, чтобы доказать выполнимость формулы, нужно указать хотя бы один набор значений пропозиционных переменных, при котором формула принимает истинное значение.

Например, доказать выполнимость следующей формулы:

.

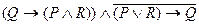Доказательство: Данная формула может быть истинной только в том случае, когда обе компоненты конъюнкции принимают значение «истина», т.е. когда , .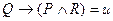

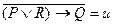Последнее утверждение возможно, когда . Последняя импликация ложна тогда и только тогда, когда посылка истинна, а заключение ложно, т.е. когда , 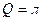. Если 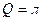, тогда первая компонента конъюнкции 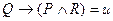, для любых значений переменных 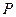и 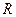. Значит, существует набор значений пропозиционных переменных, входящих в формулу, при котором она принимает истинное значение. Например, 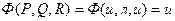. Таким образом, рассмотренная формула является выполнимой.

Определение 6: Формулы 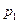и 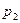называются равносильными (логически эквивалентными), если при любом наборе значений пропозиционных переменных формулы 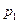и 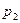принимают одинаковые истинностные значения.

Приведём некоторые равносильности алгебры высказываний, которые выражают связь между различными логическими операциями.

 

Зависимости между различными логическими операциями:

 

1) ,

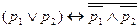2) ,

3) ,

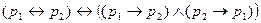4) ,

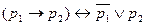5) ,

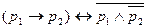6) ,

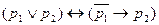7) ,

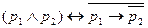8) ,

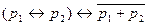9) .

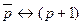Данные равносильности также можно доказывать несколькими способами: а) метод истинностных таблиц (у равносильных формул таблицы истинности совпадают построчно), б) метод равносильных преобразований, в) с помощью рассуждений.

Докажем выборочно некоторые равносильности.

(4) Построим таблицу истинности для данной формулы:

 

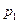
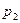
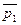
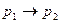
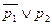
и	и	л	и	и
и	л	л	л	л
л	и	и	и	и
л	л	и	и	и

 

Последние две колонки, соответствующие левой и правой частям эквивалентности, совпадают. Значит, формулы, записанные в этих колонках, являются равносильными.

Таким образом, равносильные формулы будут иметь одинаковые таблицы истинности и наоборот, формулы, таблицы истинности которых совпадают, равносильны. Этим можно пользоваться на практике для установления равносильности формул.

Докажем это же утверждение (4) с помощью рассуждений.

Пусть 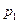и 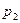– произвольные высказывания. Импликация 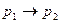ложна в одном случае, когда 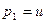, 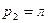. Дизъюнкция 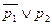ложна, если оба высказывания 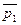и 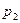– ложны, т. е. 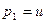, 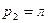. Таким образом, 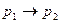и 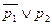оба ложны тогда и только тогда, когда 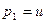, 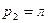. В остальных случаях оба высказывания всегда истинны. Значит, при любом наборе значений пропозиционных переменных данные формулы принимают одинаковые истинностные значения, т. е. эквивалентны.

Остальные равносильности можно доказать аналогично.

 

Теорема 4: (Условие равносильности формул исчисления высказываний):

Две формулы исчисления высказывани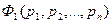й и 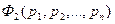, образованные с помощью одних и тех же пропозиционных букв, равносильны тогда и только тогда, когда эквивалентность этих высказываний 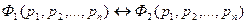является тавтологией.