Алгоритм преобразования произвольной формулы в СНДФ.
1) Выразить все логические операции через конъюнкцию, дизъюнкцию и отрицание.
2) Используя дистрибутивные законы, преобразовать формулу так, чтобы все конъюнкции выполнялись раньше дизъюнкций, а отрицания относились только к простым переменным.
3) Если имеется несколько одинаковых элементарных конъюнкций, то оставляем только одну из них (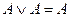 ).
).
4) Если в некоторую элементарную конъюнкцию входит переменная со своим отрицанием, то удаляем эту конъюнкцию (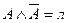 , а
, а  ).
).
5) Если в какую-то элементарную конъюнкцию не входит какая-либо переменная, то добавляем её дизъюнктивно, т. е. с помощью соотношений: 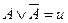 ,
, 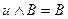 . Затем снова возвращаемся к пункту 2).
. Затем снова возвращаемся к пункту 2).
Аналогично можно составить алгоритм получения СНКФ. Для примера преобразуем к виду СНКФ уже рассмотренную формулу  .
.
Имеем:  =
= 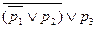 =
= 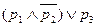 =
= 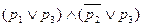 =
=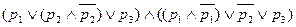 = =
= =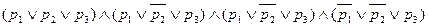 = =
= =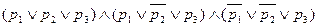 .
.
Следует отметить, что в каждую скобку СНКФ и СНДФ должны входить все переменные (с отрицанием или без него), входящие в исходную формулу. СНДФ (СНКФ) можно рассматривать как частные случаи ДНФ (КНФ). ДНФ (дизъюнктивная нормальная форма) – это дизъюнкция элементарных конъюнкций (как и СНДФ). Отличие состоит в том, что для ДНФ в каждую элементарную конъюнкцию не обязательно входят все переменные. ДНФ может быть получена с помощью пунктов 1-4 алгоритма. Аналогично для КНФ. В отличие от совершенных форм, ДНФ (КНФ) могут быть не единственными.
Определение 5: Система логических операций называется полной, если всякую формулу алгебры логики можно представить только через операции данной системы.
Теорема: Система логических операций 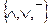 полна.
полна.
Доказательство. Выше было показано, что любую формулу алгебры логики можно представить в виде СНДФ или в виде СНКФ, где используются только конъюнкция, дизъюнкция и отрицание. Теорема доказана.
Так как дизъюнкция выражается через конъюнкцию и отрицание, а конъюнкция выражается через дизъюнкцию и отрицание, то следующие системы логических операций тоже являются полными: 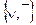 и
и 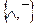 . Кроме того, конъюнкция и дизъюнкция могут быть выражены через импликацию и отрицание, поэтому система логических операций
. Кроме того, конъюнкция и дизъюнкция могут быть выражены через импликацию и отрицание, поэтому система логических операций 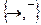 также полна.
также полна.
Все эти рассуждения можно продемонстрировать на примере:
 =
= 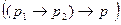 =
= 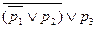 =
= 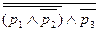 .
.