Пространство всех решений однородной системы уравнений. Фундаментальный набор решений однородной системы линейных уравнений.
Теорема 1. Пусть (1)  - однородная система линейных уравнений над полем P, U – множество всех решений системы (1), т.е. U=
- однородная система линейных уравнений над полем P, U – множество всех решений системы (1), т.е. U=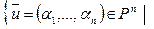
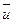 - решение системы (1)
- решение системы (1) . Тогда множество U является подпространством векторного пространства V=Pn.
. Тогда множество U является подпространством векторного пространства V=Pn.
Доказательство проводится непосредственной проверкой с помощью критерия подпространства.
Определение 1. Пусть (1)  - однородная неопределенная система линейных уравнений над полем P, U – векторное пространство всех решений системы (1). Базис векторного пространства U называется фундаментальным набором решений однородной системы линейных уравнений (1).
- однородная неопределенная система линейных уравнений над полем P, U – векторное пространство всех решений системы (1). Базис векторного пространства U называется фундаментальным набором решений однородной системы линейных уравнений (1).
Найдём фундаментальный набор решений системы (1). Пусть x1,…,xr – главные неизвестные, остальные – свободные неизвестные.
Составим систему векторов из U по следующему правилу (*): придадим первой свободной неизвестной значение 1, остальным свободным неизвестным – значение 0, получим вектор  ; придадим второй свободной неизвестной значение 1, остальным свободным неизвестным – значение 0, получим вектор
; придадим второй свободной неизвестной значение 1, остальным свободным неизвестным – значение 0, получим вектор  , и т.д. Получим систему вида:
, и т.д. Получим систему вида:
(2)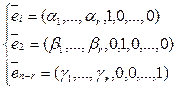 . Покажем, что (2) – базис векторного пространства U.
. Покажем, что (2) – базис векторного пространства U.
1) Покажем, что система (2) линейно независима. Пусть (3)  . Покажем, что
. Покажем, что 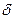 i=0, i=1,
i=0, i=1, . Подставим в (3) значения из (2). Получим
. Подставим в (3) значения из (2). Получим
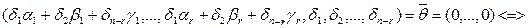
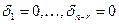 . Это означает, что система (2) линейно независима.
. Это означает, что система (2) линейно независима.
2) Покажем, что через векторы системы (2) линейно выражается каждый вектор из U. Пусть  . Покажем, что вектор
. Покажем, что вектор 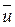 линейно выражается через векторы системы (2). Рассмотрим вектор
линейно выражается через векторы системы (2). Рассмотрим вектор  следующего вида:
следующего вида:

Так как (2)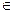 U , то
U , то 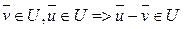 . Поскольку
. Поскольку 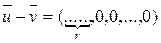 и (1) - однородная система линейных уравнений, то
и (1) - однородная система линейных уравнений, то  =>
=> 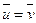 =>
=> 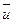 линейно выражается через (2).
линейно выражается через (2).
Из 1) и 2) следует, что система (2) – базис пространства U и, значит, система (2) удовлетворяет определению фундаментального набора решений системы (1).
Вывод: Для того, чтобы найти фундаментальный набор решений однородной системы линейных уравнений, необходимо решить систему методом Гаусса и записать систему 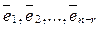 по правилу (*).
по правилу (*).