рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства
Реферат Курсовая Конспект
Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства
Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства - раздел Математика, 2. Матрицы. Основные Определения – Прямоугольная, Квадратная, Диагона...
2. Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства.
Определение 1. Матрицей размера m×n над полем Р называется прямоугольная таблица, состоящая из n строк и m столбцов, следующего вида:
 , где aij
, где aij 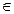 P, i=
P, i=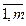 , j=
, j=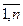 .
.
Определение 2. Квадратной матрицей n-го порядка над полем P называется матрица размера n×n над полем P.
Пусть A – квадратная матрица n-го порядка. Тогда в А выделяют 2 диагонали: главную и побочную.
 | |||
 |

главная побочная
Матрицы обозначаются следующим образом: А=(aij) или А=||aij||, i=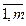 , j=
, j=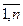 .
.
Определение 3. Элементы aii квадратной матрицы А=(aij) называются диагональными, или элементами главной диагонали.
Определение 4. Квадратная матрица А=(aij) называется диагональной, или все ёё элементы, кроме элементов главной диагонали, равны нулю: aii≠ 0, aij=0 при i≠j.
Через Аi будем обозначать i-ю строку матрицы А, т.е. Аi=(ai1 ai1 … ain), через Аj – j-й столбец матрицы А, т.е. Аj = .
.
Определение 5. Матрица А=(aij), i=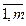 , j=
, j=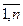 называется треугольной (верхней треугольной), если aij=0 при i>j.
называется треугольной (верхней треугольной), если aij=0 при i>j.
Строку или столбец матрицы А называют нулевыми, если все их элементы равны нулю.
Определение 6. Матрица А=(aij), i=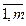 , j=
, j=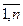 называется ступенчатой (матрицей ступенчатого вида), если во всех ее строках вторые индексы первых слева ненулевых элементов
называется ступенчатой (матрицей ступенчатого вида), если во всех ее строках вторые индексы первых слева ненулевых элементов 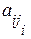 возрастают j1<j2<…<ji.
возрастают j1<j2<…<ji.
Из определения 6 следует, что ступенчатая матрица является треугольной, причем ее нулевые строки (если они есть) расположены ниже ее ненулевых строк.
Определение 7. Две матрицы A=(aij) и B=(bij) размера m×n над полем P называются равными, если aij=bij, i= , j=
, j=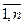 . Обозначается А=В.
. Обозначается А=В.
Определение 8. Матрица над полем P называется нулевой, если все ее элементы равны нулю. Обозначается 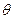 =
= .
.
Определение 9. Матрица n-го порядка вида  называется единичной матрицей. Другими словами, единичная матрица — это диагональная матрица у которой все элементы главной диагонали равны 1: aii=1 для всех i.
называется единичной матрицей. Другими словами, единичная матрица — это диагональная матрица у которой все элементы главной диагонали равны 1: aii=1 для всех i.
Определение 10. Пусть A=(aij), B=(bij) - матрицы размера m×n над полем Р. Суммой матриц А и В называется матрица С=(cij) размера m×n над полем Р, где cij=aij+bij, i=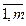 , j=
, j=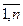 , и обозначается С=А+В.
, и обозначается С=А+В.
Теорема. Для любых матриц А , В и С размера m×n над полем P выполняются следующие свойства: 1) А+В=В+А; 2) А+(В+С)=(А+В)+С; 3) А+ =
= +А=А; 4) для любой матрицы А над полем P существует матрица (-А) такая, что А+(-А)=-А+А=
+А=А; 4) для любой матрицы А над полем P существует матрица (-А) такая, что А+(-А)=-А+А= .
.
Доказательство. Так как сложение матриц сводится к сложению элементов поля Р, а в поле Р сложение коммутативно и ассоциативно, существует нулевой элемент и для каждого элемента есть противоположный, то эти свойства выполняются и для матриц.
Множество всех матриц размера m×n над полем P обозначается через Мm,n(Р). Из теоремы следует, что Мm,n(Р) является аддитивной абелевой группой.
Умножение матрицы на скаляр, транспонирование матриц, умножение матриц и их основные свойства.
Определение 2. Пусть A=(aij) – матрица размера m×n над полем P, B=(bij) - матрица размера n×k над полем P. Произведением матриц А и В… Лемма 1. Пусть А, В, С - матрицы над полем Р. Если существует произведение… Доказательство. Пусть существует произведение (АВ)С. Тогда существуют матрицы АВ размера m×n и матрица С размера…Разложение определителя по ряду. Минор и алгебраическое дополнение к элементу определителя. Связь алгебраических дополнений с минорами.
Определение 1. Если в определителе Δ сгруппировать все слагаемые, содержащие элемент aij и, сгруппировав, вынести элемент aij за скобки, то… Так как все элементы i-той строки определителя Δ входят в одно и только… Аналогично: Δ=a1jA1j+ a2jA2j+ … + anjAnj (2) - разложение определителя Δ по j-тому столбцу, j =.Системы линейных уравнений (СЛУ). Решение системы линейных уравнений. Элементарные преобразования СЛУ. Элементарные преобразования матрицы.
Определение 2. Упорядоченная n-ка (), где , называется решением системы линейных уравнений (1), если при замене переменной на каждое уравнение… Определение 3. Система линейных уравнений (1) называется совместной, если она… Определение 4. Система линейных уравнений (1) называется определенной, если она имеет единственное решение. В…Формула для вычисления обратной матрицы.
Если определитель =0, то А-1, причем А-1=, где Аij - алгебраическое дополнение к элементу аij в матрице А, i=, j=. Доказательство. Так как А – невырожденная матрица. Тогда, по теореме 3, А –… АВ==Формулы Крамера.
Доказательство. Пусть Х=, В=. Тогда система (1) равносильна матричному уравнению АХ=В (2). Следовательно, чтобы решить систему (1), достаточно решить уравнение (2). Так как 0, то существует А-1 и уравнение (2)…Определение векторного пространства. Примеры векторных пространств. Арифметическое n-мерное векторное пространство.
Пусть Р – поле. Элементы a, b, ... ÎР будем называть скалярами.
Определение 1. Класс V объектов (элементов)  ,
, 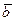 ,
, 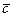 , ... произвольной природы называется векторным пространством над полем Р, а элементы класса V называются векторами, если V замкнуто относительно операции «+» и операции умножения на скаляры из Р (т.е. для любых
, ... произвольной природы называется векторным пространством над полем Р, а элементы класса V называются векторами, если V замкнуто относительно операции «+» и операции умножения на скаляры из Р (т.е. для любых  ,
, 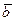 ÎV
ÎV  +
+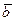 ÎV;"aÎ Р
ÎV;"aÎ Р a
a ÎV), и выполняются следующие условия:
ÎV), и выполняются следующие условия:
А1: алгебра <V, +> - абелева группа;
А2: для любых a, bÎР, для любого  ÎV выполняется a(b
ÎV выполняется a(b )=(ab)
)=(ab) - обобщенный ассоциативный закон;
- обобщенный ассоциативный закон;
А3: для любых a, bÎР, для любого  ÎV выполняется (a+b)
ÎV выполняется (a+b) = a
= a + b
+ b ;
;
А4: для любого a из Р, для любых  ,
, 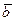 из V выполняется a(
из V выполняется a( +
+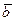 )=a
)=a +a
+a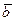 (обобщённые дистрибутивные законы);
(обобщённые дистрибутивные законы);
А5: для любого  из V выполняется 1
из V выполняется 1  =
=  , где 1 – единица поля Р — свойство унитарности.
, где 1 – единица поля Р — свойство унитарности.
Элементы поля Р будем называть скалярами, а элементы множества V — векторами.
Замечание. Умножение вектора на скаляр не является бинарной операцией на множестве V, так как это отображение P´V®V.
Рассмотрим примеры векторных пространств.
Пример 1. Нулевое (нуль-мерное) векторное пространство — пространство V0={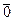 } — состоящее из одного нуль-вектора.
} — состоящее из одного нуль-вектора.
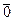 +
+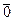 =
=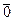 и для любого aÎР a
и для любого aÎР a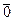 =
=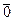 . Проверим выполнимость аксиом векторного пространства.
. Проверим выполнимость аксиом векторного пространства.
Заметим, что нулевое векторное пространство существенно зависит от поля Р. Так, нульмерные пространства над полем рациональных чисел и над полем действительных чисел считаются различными, хоть и состоят из единственного нуль-вектора.
Пример 2. Поле Р само является векторным пространством над полем Р. Пусть V=P. Проверим выполнимость аксиом векторного пространства. Так как Р — поле, то Р является аддитивной абелевой группой и А1 выполняется. В силу выполнимости в Р ассоциативности умножения выполняется А2. Аксиомы А3 и А4 выполняются в силу выполнимости в Р дистрибутивности умножения относительно сложения. Так как в поле Р существует единичный элемент 1, то выполняется свойство унитарности А5. Таким образом, поле Р является векторным пространством над полем Р.
Пример 3.Арифметическое n-мерное векторное пространство.
Пусть Р — поле. Рассмотрим множество V= Pn ={(a1, a2, … , an) ½ ai Î P, i=1,…, n}. Введём на множестве V операции сложения векторов и умножения вектора на скаляр по следующим правилам:
" = (a1, a2, … , an),
= (a1, a2, … , an), 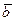 = (b1, b2, … , bn) Î V, "aÎ P
= (b1, b2, … , bn) Î V, "aÎ P  +
+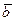 = (a1 + b1, a2+ b2, … , an+ bn) (1)
= (a1 + b1, a2+ b2, … , an+ bn) (1)
a =(aa1, aa2, … , aan) (2)
=(aa1, aa2, … , aan) (2)
Элементы множества V будем называть n-мерными векторами. Два n-мерных вектора называются равными, если их соответствующие компоненты (координаты) равны. Покажем, что V является векторным пространством над полем Р. Из определения операций сложения векторов и умножения вектора на скаляр следует, что V замкнуто относительно этих операций. Так как сложение элементов из V сводится к сложению элементов поля Р, а Р является аддитивной абелевой группой, то и V является аддитивной абелевой группой. Причём, 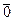 =
= 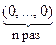 , где 0 — ноль поля Р, -
, где 0 — ноль поля Р, - = (-a1, -a2, … , -an). Таким образом, А1 выполняется. Так как умножение элемента из V на элемент из Р сводится к умножению элементов поля Р, то:
= (-a1, -a2, … , -an). Таким образом, А1 выполняется. Так как умножение элемента из V на элемент из Р сводится к умножению элементов поля Р, то:
— А2 выполняется в силу ассоциативности умножения на Р;
— А3 и А4 выполняются в силу дистрибутивности умножения относительно сложения на Р;
— А5 выполняется, так как 1 Î Р — нейтральный элемент относительно умножения на Р.
Определение 2. Множество V= Pn с операциями, определёнными формулами (1) и (2) называется арифметическим n-мерным векторным пространством над полем Р.
Простейшие свойства векторного пространства
Свойство 1. Для любого из V 0×= , где 0 — ноль поля Р, — нулевой элемент аддитивной группы V, т. е. ноль-вектор. Доказательство. 0×= (0 + 0) = А4 = 0×+ 0×, т.е. 0×=… С другой стороны 0×= 0×+ (2)Линейная комбинация системы векторов. Линейно зависимая и линейно независимая системы векторов.
Определение 2. Вектор ÎV называется линейной комбинацией системы векторов (1), если существуют скаляры a1, a2,..., aк Î P такие, что =… Определение 3. Система векторов называется линейно зависимой, если по крайней… Теорема.Система векторов (1) является линейно зависимой тогда и только тогда, когда существуют скаляры a1, a2,..., aк…Свойства линейно зависимой системы векторов.
Свойство 1. Система векторов, содержащая линейно зависимую подсистему, является линейно зависимой. Доказательство. Пусть , , …, - линейно зависимая подсистема системы векторов … , , …, (1). Тогда по определению существуют скаляры a1, a2,..., alÎР, не равные нулю одновременно, такие, что…Базис системы векторов. Координаты вектора в данном базисе. Разложение вектора по базису — существование и единственность.
Определение 1. Максимальная линейно независимая подсистема системы векторов (1) называется базисом этой системы. Теорема. Если система (2) , , …, — базис системы векторов (1), то любой вектор… Доказательство. Пусть — некоторый вектор из системы векторов (1). Если принадлежит базису (2), то =для некоторого…Теорема о том, что любые два базиса системы векторов состоят из одного и того же числа векторов. Ранг системы векторов. Конечномерные векторные пространства. Примеры.
Теорема 1. Любые два базиса системы векторов (1) 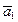 ,
, 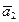 , …,
, …, 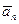 состоят из одного и того же числа векторов.
состоят из одного и того же числа векторов.
Доказательство. Пусть системы (2) 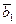 ,
, 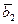 ,…,
,…, 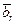 и (3)
и (3) 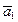 ,
, 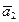 , …,
, …, 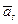 — различные базисы системы векторов (1). Допустим, что r¹s. Возможны два случая: s > r или s < r. Пусть s > r. Т.к. (2) — базис системы векторов (1), то по определению любой вектор системы векторов (1) является линейной комбинацией базисных векторов системы (2), и, в частности, каждый вектор системы (3) является линейной комбинацией векторов системы (2), поскольку система векторов (3) является подсистемой системы векторов (1). Т.к. s > r, то получили, что большая система векторов (3) линейно выражается через меньшую систему векторов (2) и, значит, по свойствам линейно зависимой системы векторов, система (3) является линейно зависимой. Получили противоречие с тем, что система (3) является базисом и, следовательно, линейно независима. Это означает, что s не больше r.
— различные базисы системы векторов (1). Допустим, что r¹s. Возможны два случая: s > r или s < r. Пусть s > r. Т.к. (2) — базис системы векторов (1), то по определению любой вектор системы векторов (1) является линейной комбинацией базисных векторов системы (2), и, в частности, каждый вектор системы (3) является линейной комбинацией векторов системы (2), поскольку система векторов (3) является подсистемой системы векторов (1). Т.к. s > r, то получили, что большая система векторов (3) линейно выражается через меньшую систему векторов (2) и, значит, по свойствам линейно зависимой системы векторов, система (3) является линейно зависимой. Получили противоречие с тем, что система (3) является базисом и, следовательно, линейно независима. Это означает, что s не больше r.
Допустим, что s < r. Проводя аналогичные рассуждения, получим, что большая система векторов (2) является линейной комбинацией меньшей системы векторов (3). Значит, по основной лемме о линейной зависимости, система векторов (2) линейно зависима. Получили противоречие с определением базиса. Таким образом, s не меньше r. Получили, что s = r. Теорема доказана.
Определение 1. Число r векторов в базисе системы векторов (1) называется рангом системы векторов (1) и обозначается r = rang {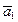 ,
, 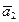 , …,
, …, 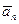 } или r = r{
} или r = r{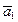 ,
, 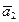 , …,
, …, 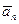 }.
}.
Определение 2. Векторное пространство V над полем P называется конечномерным векторным пространством, если существует конечная линейно независимая система векторов (1) 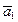 ,
, 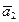 , …,
, …, 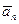 из V такая, что каждый вектор из V является линейной комбинацией системы векторов (1). При этом система векторов (1) называется базисом конечномерного векторного пространства V.
из V такая, что каждый вектор из V является линейной комбинацией системы векторов (1). При этом система векторов (1) называется базисом конечномерного векторного пространства V.
Теорема 2. Любые два базиса конечномерного векторного пространства V состоят из одного и того же числа векторов.
Доказательство проводится аналогично доказательству теоремы 1.
Определение 3. Число n векторов в базисе конечномерного векторного пространства V называется размерностью векторного пространства V над полем P и обозначается n = dimРV. В этом случае V называется n-мерным векторным пространством над полем P и обозначается Vn.
Примеры.1) n, n,ℂn, Pn — примеры классических арифметических n-мерных векторных пространств над полями соответственно , , ℂ и Р.
2) Тn — множество всех многочленов степени не выше n с коэффициентами из поля Р. Тn образует (n+1)-мерное векторное пространство над полем Р с базисом 1, х, х2, … , хn, т.е.
Тn= {f(x)=a01 + a1x +…+ an хn ½ aiÎP, i=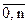 }.
}.
3) Множество прямоугольных матриц размера m´n с элементами из поля Р образует mn-мерное векторное пространство над полем Р.
4) Множество Т всех многочленов с коэффициентами из поля Р образует бесконечномерное векторное пространство над полем Р с базисом 1, х, х2, … , хn, …
В дальнейшем будем рассматривать только конечномерные векторные пространства.
Дополнение линейно независимой системы векторов векторного пространства V до базиса. Подпространство векторного пространства. Критерий подпространства. Пересечение и сумма подпространств.
Лемма 1. Любая линейно независимая система векторов векторного пространства Vn может быть дополнена до базиса пространства Vn.
Доказательство. Пусть 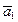 ,
, 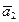 , …,
, …, 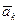 (1) — линейно независимая система векторов n-мерного векторного пространства Vn. Пусть (2)
(1) — линейно независимая система векторов n-мерного векторного пространства Vn. Пусть (2) 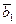 ,
, 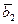 ,…,
,…, 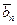 — базис пространства Vn. Рассмотрим систему векторов
— базис пространства Vn. Рассмотрим систему векторов 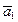 ,
, 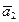 , …,
, …, 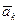 ,
, 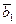 ,
, 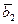 ,…,
,…, 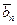 (3). Система векторов (3) конечная и она содержит максимальную линейно независимую подсистему (2). Следовательно, система векторов (2) является базисом системы векторов (3). Так как любые два базиса системы векторов (3) состоят из одного и того же числа векторов n, то в конечной системе векторов (3) можно построить максимальную линейно независимую подсистему, содержащую систему векторов (1). Тогда она будет состоять из n векторов и, значит, будет являться базисом пространства V.
(3). Система векторов (3) конечная и она содержит максимальную линейно независимую подсистему (2). Следовательно, система векторов (2) является базисом системы векторов (3). Так как любые два базиса системы векторов (3) состоят из одного и того же числа векторов n, то в конечной системе векторов (3) можно построить максимальную линейно независимую подсистему, содержащую систему векторов (1). Тогда она будет состоять из n векторов и, значит, будет являться базисом пространства V.
Определение 4. Пусть Н – непустое подмножество векторного пространства V над полем Р. Н называется подпространством пространства V, если Н само является векторным пространством над полем Р.
Теорема (критерий подпространства). Пусть Н – непустое подмножество пространства V над полем Р. Н является подпространством V тогда и только тогда, когда выполняются следующие условия:
1) Для любых  ,
,  из Н
из Н  +
+  Î Н;
Î Н;
2) для любого a из Р и любого  из Н выполняется a
из Н выполняется a Î Н.
Î Н.
Доказательство. Необходимость. Пусть Н – подпространство пространства V. Тогда по определению Н является векторным пространством над полем Р и H замкнуто относительно сложения векторов и умножения вектора на скаляр из поля Р. Следовательно, условия 1) и 2) выполняются.
Достаточность. Пусть выполняются условия 1) и 2) теоремы. Т.к. (-1)ÎР, то по условию 2) для любого  из Н (-1)
из Н (-1) = -
= -  Î Н. Тогда, по критерию подгруппы, Н является подгруппой аддитивной абелевой группы V, и, следовательно, Н само является аддитивной абелевой группой. Т.к. обобщенные дистрибутивные и ассоциативные законы выполняются в V, то они выполняются и в Н. Кроме того, 1
Î Н. Тогда, по критерию подгруппы, Н является подгруппой аддитивной абелевой группы V, и, следовательно, Н само является аддитивной абелевой группой. Т.к. обобщенные дистрибутивные и ассоциативные законы выполняются в V, то они выполняются и в Н. Кроме того, 1 =
= для любого
для любого  из Н. Следовательно, Н удовлетворяет определению векторного пространства над полем Р и, значит, по определению Н является подпространством пространства V.
из Н. Следовательно, Н удовлетворяет определению векторного пространства над полем Р и, значит, по определению Н является подпространством пространства V.
Определение 2. Пусть V1, V2,…, Vs — подпространства векторного пространства V над полем Р. Множество М={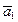 +
+ 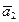 + …+
+ …+ 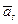 ½
½ 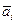 Î Vi, i=
Î Vi, i=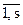 } называется суммой подпространств V1, V2,…, Vs и обозначается М = V1 + V2 +…+ Vs.
} называется суммой подпространств V1, V2,…, Vs и обозначается М = V1 + V2 +…+ Vs.
Лемма 2. Пусть V1, V2,…, Vs — подпространства векторного пространства V над полем Р. Тогда
1) Н = V1 + V2 +…+ Vs является подпространством пространства V;
2) D = V1 Ç V2 Ç…Ç Vs является подпространством пространства V.
Доказательство. 1) Пусть  ,
, 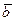 Î Н. Тогда по определению суммы подпространств
Î Н. Тогда по определению суммы подпространств
 =
=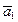 +
+ 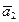 + …+
+ …+ 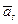 ,
, 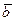 =
=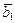 +
+ 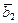 + …+
+ …+ 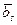 , где
, где 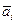 ,
, 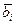 Î Vi, i=
Î Vi, i=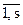 . Найдём сумму
. Найдём сумму
 +
+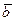 = (
= (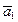 +
+ 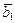 ) + (
) + (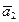 +
+ 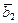 ) +…+ (
) +…+ (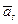 +
+ 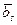 ). Так как
). Так как 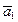 +
+ 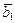 Î V1,
Î V1, 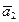 +
+ 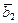 ÎV2, … ,
ÎV2, … , 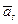 +
+ 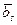 ÎVs, то по определению
ÎVs, то по определению  +
+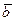 Î Н. Значит, Н замкнуто относительно сложения векторов. Далее, для любого a из Р и любого
Î Н. Значит, Н замкнуто относительно сложения векторов. Далее, для любого a из Р и любого  из Н выполняется:
из Н выполняется:
a  = a(
= a( 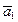 +
+ 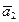 + …+
+ …+ 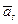 )= a
)= a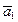 + a
+ a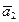 + …+ a
+ …+ a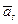 .
.
Поскольку a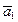 Î V1, a
Î V1, a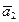 Î V2, … , a
Î V2, … , a 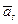 Î Vs, то по определению a
Î Vs, то по определению a Î Н и Н замкнуто относительно умножения на скаляры из поля Р. По критерию подпространства, Н является подпространством пространства V.
Î Н и Н замкнуто относительно умножения на скаляры из поля Р. По критерию подпространства, Н является подпространством пространства V.
2) Доказательство проводится аналогично.
Изоморфизм векторных пространств одинаковой размерности.
1) j(+) = j() + j() для любых и из V1; 2) j(a ) = aj( ) и для любых Î V1 и aÎР. Теорема. Пусть V — векторное пространство над полем P и dimPV=n. Тогда V@Pn, гдеPn — арифметическое n-мерное векторное…Пространство всех решений однородной системы уравнений. Фундаментальный набор решений однородной системы линейных уравнений.
Доказательство проводится непосредственной проверкой с помощью критерия подпространства. Определение 1. Пусть (1) - однородная неопределенная система линейных… Найдём фундаментальный набор решений системы (1). Пусть x1,…,xr – главные неизвестные, остальные – свободные…Связь между решениями неоднородной системы линейных уравнений с решениями ассоциированной с ней однородной системы линейных уравнений.
1) Если и - решения системы (1), то - решение системы (2). 2) Если - решение системы (1) и - решение (2), то - решение системы (1). Доказательство. 1) Так как - решение (1), то . Так как - решение (1), то . Тогда , => - решение системы (2).Линейная оболочка системы векторов. Размерность подпространства. Размерность суммы двух подпространств.
L() = называется линейной оболочкой, натянутой на векторы системы . Теорема 1. Пусть - система векторов векторного пространства V полем Р. Тогда L() является подпространством векторного…Матрица перехода от базиса к базису. Преобразование координат.
Если сложение матриц, элементами которых служат векторы, или умножение матрицы над полем на матрицу, элементы которой – векторы, производить также… Пусть - другой базис векторного пространства Vn. Векторы базиса линейно… Определение 1. Пусть Vn - n-мерное векторное пространство над полем P, (1) и (2) – базисы Vn . Матрицей перехода от…Линейные отображения, примеры. Простейшие свойства линейных отображений. Задание линейного отображения с помощью отображения базиса.
Определение 1. Пусть V и V1 – векторные пространства над полем Р. Отображение  называется линейным отображением V в V1 или гомоморфизмом, если выполняются следующие условия:
называется линейным отображением V в V1 или гомоморфизмом, если выполняются следующие условия:
1)  - условие аддитивности;
- условие аддитивности;
2)  - условие однородности.
- условие однородности.
Примеры линейных отображений
Пример 1. Пусть  - отображение, заданное по правилу:
- отображение, заданное по правилу:  , где
, где 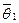 - нулевой элемент векторного пространства V1. Тогда
- нулевой элемент векторного пространства V1. Тогда
1)  ;
;
2) 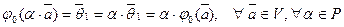 .
.
Из 1) и 2) следует, что  - линейное отображение V в V1, которое называется нулевым линейным отображением или нулевым гомоморфизмом.
- линейное отображение V в V1, которое называется нулевым линейным отображением или нулевым гомоморфизмом.
Пример 2. Пусть  - отображение, заданное по правилу:
- отображение, заданное по правилу:  . Тогда
. Тогда
1)  ;
;
2)  .
.
Из 1) и 2) следует, что  - линейное отображение V, которое называется тождественным линейным отображением или тождественным линейным оператором V.
- линейное отображение V, которое называется тождественным линейным отображением или тождественным линейным оператором V.
Теорема 1. Пусть V и V1 – векторные пространства над полем Р,  - линейное отображение V в V1. Тогда справедливы следующие утверждения:
- линейное отображение V в V1. Тогда справедливы следующие утверждения:
1)  где
где  и
и 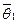 - нулевые элементы векторного пространства V и векторного пространства V1 соответственно;
- нулевые элементы векторного пространства V и векторного пространства V1 соответственно;
2) 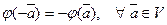 ;
;
3)  ;
;
4) если 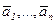 – линейно зависимая система векторов из V, то и система векторов
– линейно зависимая система векторов из V, то и система векторов  линейно зависима, при этом сохраняются все линейные соотношения между векторами, то есть если
линейно зависима, при этом сохраняются все линейные соотношения между векторами, то есть если  , то
, то  .
.
Доказательство.
1) Рассмотрим вектор 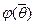 :
: 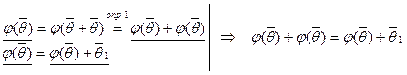 (1).
(1).
Так как V1 – аддитивная группа, то из (1) по закону сокращения получим 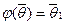 .
.
2) Рассмотрим вектор 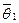 :
:  . Таким образом,
. Таким образом,  (2). Прибавим к обеим частям равенства (2) вектор
(2). Прибавим к обеим частям равенства (2) вектор  :
:  . Получаем
. Получаем  .
.
3) -4) – без доказательства.
Напомним, что отображение f: X→Y считается заданным, если указано правило, по которому можно найти f(x), 
 линейное отображение векторного пространства V в векторное пространство U будет задано, если будет определено правило, по которому
линейное отображение векторного пространства V в векторное пространство U будет задано, если будет определено правило, по которому 
 можно найти
можно найти  . Если в качестве V рассматривать конечномерное векторное пространство, то можно доказать, что для того, чтобы определить линейное отображение V в U , достаточно указать лишь образы базисных векторов.
. Если в качестве V рассматривать конечномерное векторное пространство, то можно доказать, что для того, чтобы определить линейное отображение V в U , достаточно указать лишь образы базисных векторов.
Теорема 2. Пусть Vn – n-мерное векторное пространство над полем P, U - векторное пространство над полем P,  (1) – базис пространства Vn,
(1) – базис пространства Vn, 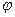 - линейное отображение Vn в U. Тогда
- линейное отображение Vn в U. Тогда 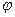 однозначно определяется заданием образов базисных векторов
однозначно определяется заданием образов базисных векторов  (2).
(2).
Из теоремы 2 следует, что линейное отображение Vn в U определяется образами базисных векторов  Так как
Так как 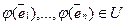 , то возникает вопрос, какие векторы из U можно взять в качестве векторов
, то возникает вопрос, какие векторы из U можно взять в качестве векторов  . Ответ на данный вопрос дает теорема 3.
. Ответ на данный вопрос дает теорема 3.
Теорема 3. Пусть Vn – n-мерное векторное пространство над полем P, U - векторное пространство над полем P,  (1) – базис Vn. Тогда любые n векторов из U можно взять в качестве образов базисных векторов при некотором линейном отображении, т.е.
(1) – базис Vn. Тогда любые n векторов из U можно взять в качестве образов базисных векторов при некотором линейном отображении, т.е.  существует единственное линейное отображение
существует единственное линейное отображение  такое, что
такое, что 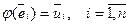 .
.
Ядро и образ, ранг и дефект линейного отображения.
Определение 2. Пусть V и V1 – векторные пространства над полем Р, - линейное отображение V в V1. Множество называется образом линейного отображения… Теорема 1. Пусть V и V1 – векторные пространства над полем Р, - линейное… 1) Множество является подпространством векторного пространства V;Связь между матрицами линейного оператора в различных базисах. Собственные векторы и собственные значения линейного оператора.
Теорема 1. Пусть Vn – n-мерное векторное пространство над полем P. Матрица Т n-го порядка над полем Р является матрицей перехода от одного базиса векторного пространства Vn к другому тогда и только тогда, когда detТ ≠ 0.
Теорема 2. Пусть Vn – n-мерное векторное пространство над полем P,  (1),
(1), 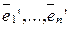 (1′) – базисы векторного пространства Vn, Т – матрица перехода от базиса (1) к базису (1′),
(1′) – базисы векторного пространства Vn, Т – матрица перехода от базиса (1) к базису (1′), 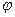 - линейный оператор векторного пространства Vn, А - матрица линейного оператора
- линейный оператор векторного пространства Vn, А - матрица линейного оператора 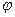 в базисе (1), В - матрица линейного оператора
в базисе (1), В - матрица линейного оператора 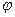 в базисе (1′). Тогда
в базисе (1′). Тогда
В=Т-1АТ.
Доказательство. Из определения матрицы линейного оператора следует, что  =
=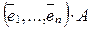 (2) и
(2) и 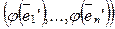 =
=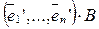 (3).
(3).
Из формул перехода от базиса к базису имеем
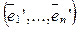 =
= (4) и
(4) и 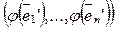 =
= (5).
(5).
Подставим из (2) и (3) соответствующие выражения в (5). Получим
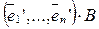 =
=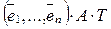 (6).
(6).
Теперь подставим в (6) вместо 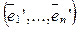 соответствующее выражение из (4):
соответствующее выражение из (4):
 =
=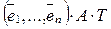 (7).
(7).
Из (7) следует, что 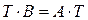 . Умножая обе части последнего равенства слева на Т-1, окончательно получим В=Т-1АТ. Теорема доказана.
. Умножая обе части последнего равенства слева на Т-1, окончательно получим В=Т-1АТ. Теорема доказана.
Определение 1. Пусть j - линейный оператор векторного пространства V над полем P. Ненулевой вектор 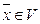 называется собственным вектором линейного оператора j, если существует lÎP такое, что
называется собственным вектором линейного оператора j, если существует lÎP такое, что
j(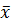 )= l
)= l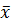 . (1)
. (1)
При этом, l называется собственным значением линейного оператора j, а 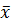 - собственным вектором линейного оператора
- собственным вектором линейного оператора  , принадлежащим собственному значению l.
, принадлежащим собственному значению l.
Лемма 1. Пусть  - собственный вектор линейного оператора
- собственный вектор линейного оператора  векторного пространства V над полем P. Если l1 и l2 - собственные значения линейного оператора j, соответствующие собственному вектору
векторного пространства V над полем P. Если l1 и l2 - собственные значения линейного оператора j, соответствующие собственному вектору 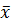 , то l1=l2.
, то l1=l2.
Доказательство. Пусть j(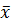 )= l1
)= l1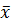 и j(
и j(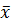 )= l2
)= l2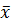 . Так как j – отображение, то l1
. Так как j – отображение, то l1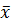 =l2
=l2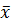 . Тогда l1
. Тогда l1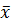 - l2
- l2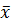 =
=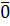 . Следовательно, (l1 - l2
. Следовательно, (l1 - l2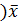 =
=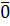 . Так как
. Так как  , то l1 - l2 и l1=l2. Лемма доказана.
, то l1 - l2 и l1=l2. Лемма доказана.
Лемма 2. Пусть P – бесконечное поле, 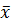 - собственный вектор линейного оператора j векторного пространства V над полем P, принадлежащий собственному значению l. Тогда существует бесконечное множество собственных векторов линейного оператора j, принадлежащих собственному значению l.
- собственный вектор линейного оператора j векторного пространства V над полем P, принадлежащий собственному значению l. Тогда существует бесконечное множество собственных векторов линейного оператора j, принадлежащих собственному значению l.
Доказательство. Для любого 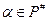 имеем
имеем 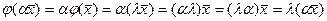 , то есть вектор
, то есть вектор 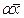 является собственным вектором линейного оператора j, принадлежащим собственному значению l. Лемма доказана.
является собственным вектором линейного оператора j, принадлежащим собственному значению l. Лемма доказана.
Нахождение собственных векторов и собственных значений линейного оператора
Пусть Vn – n-мерное векторное пространство над полем P, 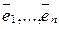 (1) – базис Vn, j - линейный оператор векторного пространства Vn. Найдём все собственные векторы и все собственные значения линейного оператора j. Пусть
(1) – базис Vn, j - линейный оператор векторного пространства Vn. Найдём все собственные векторы и все собственные значения линейного оператора j. Пусть  – собственный вектор линейного оператора j. Найдём
– собственный вектор линейного оператора j. Найдём 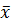 .
.
По определению j(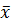 )= l
)= l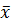 , где λ
, где λ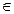 P
P 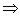
 . С другой стороны,
. С другой стороны,  . Поэтому
. Поэтому  =
= , т.е.
, т.е.  .
.
Пусть  - матрица линейного оператора j в базисе (1). Тогда
- матрица линейного оператора j в базисе (1). Тогда


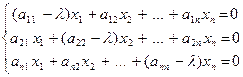 (2).
(2).
Определение 1. Система (2) называется характеристической системой линейного оператора j.
Решением системы (2) является множество всех собственных векторов линейного оператора j (за исключением нулевого решения). Решим систему (2): по правилу Крамера. Система (2) имеет единственное решение тогда и только тогда, когда определитель системы не равен нулю, т.е.  . Поскольку нас интересуют ненулевые решения системы (2), то рассмотрим случай, когда (2) неопределена, т.е. случай, когда
. Поскольку нас интересуют ненулевые решения системы (2), то рассмотрим случай, когда (2) неопределена, т.е. случай, когда  :
:
 (3).
(3).
Уравнение (3) является уравнением относительно переменной λ. Это уравнение можно записать в матричной форме:  (3).
(3).
Определение 2. Уравнение (3) называется характеристическим уравнением линейного оператора j. Многочлен f(λ)=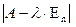 называется характеристическим многочленом линейного оператора j.
называется характеристическим многочленом линейного оператора j.
Вывод: Решая характеристическое уравнение, найдём все собственные значения l1,…, lk линейного оператора j. Подставляя li в систему (2) и решая её, получим все собственные векторы линейного оператора j, принадлежащие собственным значениям li, i = 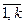 .
.
Линейные операторы с простым спектром. Условие, при котором матрица линейного оператора подобна диагональной. Приведение матрицы к диагональному виду
Определение 1. Пусть j – линейный оператор пространстваVn над полем P. Спектром линейного оператора j называется множество всех собственных значений линейного оператора j.
Определение 2. Спектр линейного оператора j называется простым, если он состоит из попарно различных собственных значений линейного оператора j.
Теорема 1. Пусть Vn – n-мерное векторное пространство над полем P, j – линейный оператор пространстваVn , l1,…, ln - спектр линейного оператора j,  - собственные векторы линейного оператора j, принадлежащие l1,…, ln соответственно. Если l1,…, ln - простой спектр, то система векторов
- собственные векторы линейного оператора j, принадлежащие l1,…, ln соответственно. Если l1,…, ln - простой спектр, то система векторов  линейно независима.
линейно независима.
Теорема 2. Пусть j - линейный оператор векторного пространства Vn над полем Р. Линейный оператор j имеет в базисе 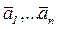 (1) матрицу диагонального вида тогда и только тогда, когда базис (1) состоит из собственных векторов линейного оператора j.
(1) матрицу диагонального вида тогда и только тогда, когда базис (1) состоит из собственных векторов линейного оператора j.
Доказательство. Необходимость. Пусть в базисе 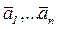 линейный оператор j имеет матрицу вида
линейный оператор j имеет матрицу вида  , где
, где 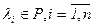 . Тогда
. Тогда  Следовательно,
Следовательно,  Так как система векторов
Так как система векторов 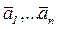 - базис, то
- базис, то  . Значит, по определению,
. Значит, по определению, 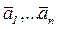 - собственные векторы линейного оператора j.
- собственные векторы линейного оператора j.
Достаточность. Пусть 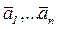 - собственные векторы линейного оператора
- собственные векторы линейного оператора  . Тогда найдутся l1,…, ln ÎР такие, что
. Тогда найдутся l1,…, ln ÎР такие, что  . Значит,
. Значит,  Следовательно, в базисе
Следовательно, в базисе 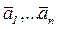 матрица линейного оператора j имеет вид
матрица линейного оператора j имеет вид  . Теорема доказана.
. Теорема доказана.
Следствие. Если линейный оператор j имеет простой спектр l1,…, ln, то в базисе, состоящем из собственных векторов линейного оператора j 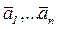 , принадлежащих соответственно собственным значениям l1,…, ln, матрица А линейного оператора j имеет вид
, принадлежащих соответственно собственным значениям l1,…, ln, матрица А линейного оператора j имеет вид  .
.
Если из собственных векторов линейного оператора j нельзя составить базис векторного пространства Vn, то ни одна из матриц линейного оператора j не имеет диагональный вид.
Приведение матрицы к диагональному виду
Пусть  - матрица n-го порядка над полем Р. Возникает вопрос: можно ли привести матрицу А к диагональному виду, то есть, будет ли матрица А подобна некоторой диагональной матрице?
- матрица n-го порядка над полем Р. Возникает вопрос: можно ли привести матрицу А к диагональному виду, то есть, будет ли матрица А подобна некоторой диагональной матрице?
Известно, что на матрицу А можно смотреть как на матрицу некоторого линейного оператора j векторного пространства V над полем Р. Тогда поставленный вопрос можно сформулировать следующим образом: найдется ли такой базис n-мерного векторного пространства V над полем Р, в котором матрица линейного оператора j будет диагональной. В общем случае ответ отрицательный. Однако, если спектр линейного оператора j простой, то матрица А приводится к диагональному виду. Если спектр матрицы имеет хотя бы одно значение, не принадлежащее полю Р, то в этом случае матрица А не приводится к диагональному виду.
Пусть  ,
, 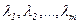 - спектр линейного оператора j. Тогда
- спектр линейного оператора j. Тогда
а) если m=n, то матрица А приводится к диагональному виду (так как в этом случае спектр линейного оператора j простой);
б) пусть m<n. В этом случае матрица А может как приводиться к диагональному виду, так и нет. Пусть 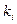 - кратность корня
- кратность корня  . Если для любого
. Если для любого 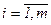 кратность
кратность 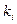 равна числу свободных неизвестных характеристической системы, соответствующей собственному значению
равна числу свободных неизвестных характеристической системы, соответствующей собственному значению  , то мы сможем найти n собственных векторов линейного оператора j, которые будут линейно независимы, и, значит, будут образовывать базис. Тогда матрица А будет приводиться к диагональному виду. В противном случае А не приводиться к диагональному виду.
, то мы сможем найти n собственных векторов линейного оператора j, которые будут линейно независимы, и, значит, будут образовывать базис. Тогда матрица А будет приводиться к диагональному виду. В противном случае А не приводиться к диагональному виду.
– Конец работы –
Используемые теги: матрицы, основные, Определения, прямоугольная, квадратная, Диагональная, треугольная, нулевая, Единичная, матрицы, Сложение, матриц, Свойства0.141
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов