Линейная оболочка системы векторов. Размерность подпространства. Размерность суммы двух подпространств.

Определение 1. Пусть V - векторное пространство над полем Р, 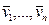—.система векторов из пространства V. Множество

L() =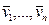

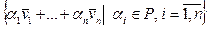
называется линейной оболочкой, натянутой на векторы системы .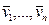

Теорема 1. Пусть 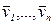- система векторов векторного пространства V полем Р. Тогда L() является подпространством векторного пространства V.

Доказательство. Пусть L=L(). Для любых имеем: 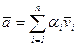, 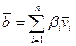. Тогда .

Далее, для любого имеем . Таким образом, по критерию подпространства получаем, что L=L() является подпространством векторного пространства V. Теорема доказана.

Теорема 2. Пусть V_n - n-мерное векторное пространство над полем P, U – его подпространство. Тогда 1)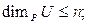

2) 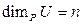тогда и только тогда, когда U = V_n.

Доказательство. 1) Так как V_n - n-мерное векторное пространство, то в V_n нет линейно независимой системы векторов, содержащей больше n векторов. Значит, и в U нет линейно независимой системы векторов, содержащей больше n векторов. Таким образом, .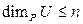

2) Необходимость. Пусть 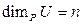. Тогда базис U содержит векторов. Так как V_n - n-мерное векторное пространство, то базис U является базисом в 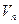. Тогда всякий вектор 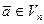можно выразить через базис U. Значит, 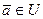. Следовательно, 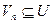и U = V_n.

Достаточность. Пусть U = V_n. Тогда 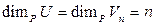. Теорема доказана.

Теорема 2. Пусть U и W - подпространства конечномерного векторного пространства V над полем P. Тогда dim_P(U+W)= dim_PU+ dim_PW- dim_P(U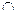W).