Матрица перехода от базиса к базису. Преобразование координат.

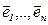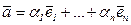Пусть V_n - n-мерное векторное пространство над полем P, (1) – базис V_n . Тогда любой вектор можно единственным образом представить в виде . Введем обозначение: - координатный вектор-столбец вектора 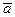в базисе .

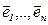Если сложение матриц, элементами которых служат векторы, или умножение матрицы над полем на матрицу, элементы которой – векторы, производить также как и соответствующие действия с матрицами над полем, то при этом останутся справедливыми все формальные свойства сложения матриц и умножения матриц на элементы поля. Тогда равенство 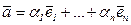равносильно матричному равенству 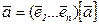. Строка называется базисной строкой. Тогда равенство 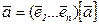означает, что вектор 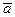есть произведение базисной строки на его координатный вектор-столбец в этом базисе.

Пусть 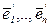- другой базис векторного пространства V_n. Векторы базиса 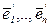линейно выражаются через векторы базиса :

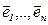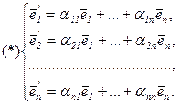
Определение 1. Пусть V_n - n-мерное векторное пространство над полем P, 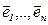(1) и 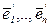(2) – базисы V_n . Матрицей перехода от базиса (1) к базису (2) называется матрица Т n-го порядка над полем Р, i-м столбцом которой является координатный вектор-столбец вектора в базисе (1), i=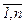, т.е. .

Из определения 1 следует, что система (*) в матричной форме имеет вид:

=(**).

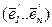Эта формула выражает связь между любыми двумя базисами пространства V.

Теорема 1. Пусть V_n - n-мерное векторное пространство над полем P, 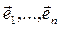(1) и () - базисы V_n, T - матрица перехода от (1) к (1^/), , - координатные вектор-столбцы вектора 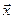в базисах (1) и (1^/) соответственно. Тогда 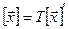(или ).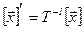

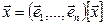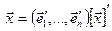Доказательство. Так как и , то 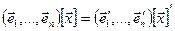. Поскольку 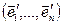=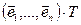, то 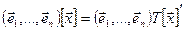. Это означает, что 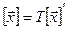. Теорема доказана.