Элементы теории вероятностей

Случайное событие, называемое также событием, – это такое явление, которое может либо произойти, либо не произойти в результате испытания.

Классическое определение вероятности.Если множество всех элементарных исходов конечно и все исходы равновозможны, то вероятность события А определяется как

где – число исходов, благоприятных для А, – общее число всех возможных элементарных исходов.

Событие, вероятность которого равна 1, называется достоверным, событие, вероятность которого равна нулю, – невозможным. Вероятность события А и противоположного ему события 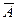связаны соотношением

События называются несовместными, если одновременное их осуществление невозможно, в частности, А и 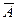несовместны.

Для любых событий А и В

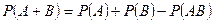для трех событий

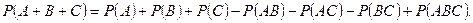
Условная вероятность события А, т.е. вероятность события А, которую находят в предположении, что событие B уже наступило, определяется формулой

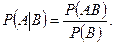
События А и В называются независимыми, если .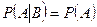

Задача 9. В ящике содержится 7 одинаковых, тщательно перемешанных шаров, причем 4 из них – красные, 2 – синие и 1– белый. Наудачу вынимается один шар. Найдем вероятность того, что вынутый шар а) синий, б) белый, в) цветной.

Решение

Появление синего шара будем рассматривать в качестве события А, появление белого шара – в качестве события В и появление цветного шара – в качестве события С.

Возможны следующие 7 равновозможных исходов испытания (извлечения шара из ящика): В₁ – появился белый шар, В₂, В₃ ,В ₄, B₅ – появился красный шар, В₆, В₇ – появился синий шар, т.е.

Событию А благоприятствуют исходы В₆ и В₇ (два исхода), событию В благоприятствует один исход В₁, а событию С – исходы В₂, В₃, В₄, В₅, В₆, В₇, (шесть исходов). Находим

,,.

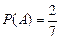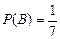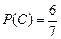Задача 10. Бросается игральная кость. Определить:

а) вероятность появления верхней грани с цифрой 4;

б) вероятность того, что выпадет нечетное число очков

Решение

а) Пусть событие А – появление верхней грани с цифрой 4. Кость имеет шесть граней, и при бросании может стать верхней любая из шести граней. Следовательно, число возможных элементарных исходов опыта . Из шести граней только одна соответствует цифре 4, поэтому число благоприятных исходов опыта 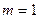. Следовательно, получим:

б) Пусть событие В – выпадение на верхней грани нечетного числа очков. Число возможных элементарных исходов опыта . Только три цифры являются нечетными: 1, 3 и 5, следовательно . Таким образом, получим:

Ответ: а) вероятность появления верхней грани с цифрой 4 равна ;

б) вероятность того, что выпадет нечетное число очков, равна .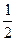

Задача 11. Отдел технического контроля обнаружил 5 бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг.

Решение

Относительная частота события А (появления бракованных книг) равна отношению числа испытаний, в которых появилось событие А, к общему числу испытаний:

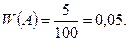
Ответ: относительная частота появления бракованных книг равна 0,05.

Задача 12. В урне 2 белых, 3 красных и 5 синих одинаковых по размеру шаров. Какова вероятность, что шар, наугад вынутый из урны (без возращения), будет красным или синим?

Решение

Пусть событие А – извлечение из урны красного шара; событие В – извлечение из урны синего шара. Тогда событие – извлечение из урны красного или синего шара. События А и В – несовместны, поэтому Имеем:

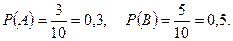
Тогда .

Ответ: вероятность, что шар, наугад вынутый из урны (без возращения), будет красным или синим, равна 0,8.

Схема независимых испытаний (схема Бернулли). Проводится независимых испытаний, в каждом из которых может произойти один из двух исходов: успех или неуспех. Вероятность успеха в каждом из этих испытаний постоянна и равна 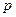. Вероятность неуспеха в одном испытании равна .

Вероятность того, что в испытаниях будет ровно т успехов, дается формулой Бернулли:

где 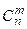– число сочетаний из n по m.

Пусть задано множество, состоящее из элементов. Каждое его неупорядоченное подмножество, содержащее элементов, называется сочетанием из элементов по элементов.

Число всех сочетаний из элементов по элементов обозначается («С (це) из по ). Для числа сочетаний справедлива формула:

В указанной формуле произведение всех натуральных чисел от 1 до обозначается ! («(эн) факториал), т.е. !=.

Задача 13. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?

Решение

Играют равносильные шахматисты, поэтому вероятность выигрыша 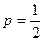; следовательно, вероятность проигрыша 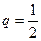. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выигрываться партии, то применима формула Бернулли.

Найдем вероятность того, что две партии из четырех будут выиграны:

Найдем вероятность того, что три партии из шести:

Так как 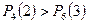, то вероятнее выиграть две партии из четырех, чем три из шести.

Ответ: вероятнее выиграть две партии из четырех, чем три из шести.

Задача 14. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.

Решение

По условию вероятность рождения мальчика 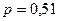, тогда вероятность противоположного события (вероятность рождения девочки) . Для нахождения искомых вероятностей применим формулу Бернулли:

а) вероятность того, что среди пяти детей два мальчика, равна:

б) вероятность того, что среди этих детей не более двух мальчиков (в семье нет мальчиков или в семье один мальчик или в семье два мальчика) , равна:

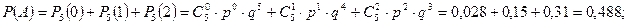
в) вероятность того, что среди пятерых детей не менее одного и не более трех мальчиков (в семье один мальчик или в семье два мальчика или в семье три мальчика), равна:

Ответ: вероятность того, что среди этих детей: а) два мальчика равна 0,31 б) не более двух мальчиков равна 0,488; в) не менее двух и не более трех мальчиков равна 0,71.