Постановка задачі

У процесі вивчення різних питань еконо­міки, природознавства, техніки тощо доводиться розв’язувати систе­ми лінійних алгебраїчних рівнянь. Зокрема, до таких систем зводи­ться чисельне розв’язування лінійних диференціальних та інтеграль­них рівнянь, за допомогою яких описують реальні процеси. Розглянемо систему n лінійних рівнянь з n змінними:

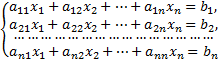, (8)

де х₁, x₂, x_n – невідомі, a_ij - коефіцієнти при невідомих, b_i - вільні члени (або праві частини).

Розв’язком системи (8) називається така впорядкована сукуп­ність чисел c₁,c₂,…,c_n, яка, будучи підставленою в (8) замість змін­них x₁,x₂,...,x_n, перетворює всі рівняння в числові тотожності.

Методи розв’язування систем лінійних алгебраїчних рівнянь мож­на розбити на дві групи: точні й наближені.

Метод називається точним, якщо він дає змогу знайти точний розв’язок системи (8) за допомогою скінченної кількості арифмети­чних операцій. При цьому припускається, що всі обчислення вико­нуються точно, а коефіцієнти системи і вільні члени - точні числа. Проте, в процесі практичних обчислень майже завжди доводиться вдаватися до заокруглення чисел, а при наявності ірраціональних коефіцієнтів і вільних членів виникає необхідність заміни їх на ра­ціональні числа. Тому розв’язки, які знайдені за допомогою точних методів, часто є наближеними числами з певними похибками. До точних належать метод Гауса, метод квадратних коренів, правило Крамера та інші.

Метод називається наближеним (або ітераційним), якщо він дає змогу знайти наближений розв’язок системи (8) із наперед заданою точністю шляхом виконання скінченної кількості арифметичних опе­рацій (навіть, якщо обчислення проводитимуться без заокруглень, а коефіцієнти і вільні члени системи будуть точними числами). Точний розв’язок системи (8) за допомогою ітераційного методу можна зна­йти тільки теоретично як границю збіжної числової послідовності. Розв’язок системи, знайдений за допомогою якого-небудь наближе­ного методу, крім похибок заокруглення, як правило, містить похиб­ки самого методу. До наближених належать метод ітерацій, метод Зейделя та інші.

В прикладних задачах коефіцієнти і вільні члени рівнянь задають, як правило, наближено. Це призводить до появи додаткових, так зва­них неусувних похибок, які слід враховувати в процесі обчислень і при остаточному заокругленні результату.