Нтерполяція
Під апроксимацією розуміють операцію знаходження невідомих чисельних значень якоїсь величини за відомими її значеннями і чисельними значеннями інших величин, які пов’язані з розглядуваною.
Інтерполяція - частковий випадок апроксимації. Нехай в точках х0, х1, х2, … , хn відомі значення f(x0), f(x1), f(x2)… f(xn) деякої функції f(x). Потрібно відновити функцію f(x) при інших значеннях х ≠ хі (і = 0, 1, 2, … , n). У цьому випадку будують достатньо просту для обчислення функцію φ(х), яка в заданих точках х0, х1, х2, … , хn приймає значення f(x0), f(x1), f(x2), …, f(xn), а в решті точках відрізку [a, b] (область визначення f(x) ), наближено представляє f(x) з деякою точністю. Задача побудови φ(х) називається задачею інтерполювання. Найчастіше інтерполюючу функцію φ(х) виражають через алгебраїчний многочлен деякої степені n.
Якщо аргумент х знаходиться зовні відрізку [a, b], то поставлена задача називається екстраполюванням (екстраполяція).
Інтерполяція в цьому випадку називається алгебраїчною. Алгебраїчне інтерполювання функції y = f(x) на відрізку [a, b] полягає в наближеній заміні цієї функції на даному відрізку многочленом Рn(х) степені n, тобто
f(x) ≈ Рn(х), (14)
причому в точках х0, х1, х2, … , хn, f(xі) = Рn(хі), (і=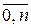 ).
).
Відмітимо, що двох різних інтерполяційних многочленів одної й тої ж степені n існувати не може. Якщо вважати протилежне, приходимо до висновку, що різниця двох таких многочленів, що є многочленом степені не вище n, має n + 1 корінь, а отже тотожно дорівнює нулю.