Метод найменших квадратів

Маємо таблицю значень:

х₁ х₂ … х_n

у₁ у₂ … у_n

 

Необхідно знайти наближену залежність у = f(x), значення якої при х = х_і (і=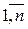), мало відрізняються від дослідних даних у_і. Наближена функціональна залежність у = f(x), яка одержана на основі експериментальних даних, називається емпіричною формулою.

Одним із способів одержання емпіричних формул є метод найменших квадратів (МНК). Будем вважати, що тип емпіричної формули відомий (це, наприклад, пряма, парабола, многочлен чи інше) і її можна зобразити у вигляді

у = j(х, а₀, а₁, … , а_m), (15)

де j - відома функція;

а₀, а₁, … , а_m – невідомі сталі параметри.

Задача полягає в тому, щоб визначити такі значення цих параметрів, при яких емпірична формула дає достатньо добре наближення таблично заданої функції.

Ідея МНК полягає в наступному. Запишемо суму квадратів відхилень для всіх точок х_і (і=)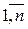

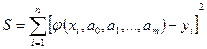(16)

Параметри а₀, а₁, … , а_m емпіричної формули (15) будем шукати з умови min функції

S = S(а₀, а₁, … , а_m). Оскільки тут параметри а₀, а₁, … , а_m виступають в ролі незалежних змінних функції S, то її min знайдемо, прирівнюючи до нуля частинні похідні за цими змінними

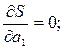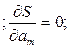… (17)

Розглянем випадок, коли за емпіричну функцію вибирають многочлен

j(х)= а₀ + а₁х + а₂х² + … + а_mх^m (18)

 

 

Тоді формула визначення суми квадратів відхилень S зобразиться так

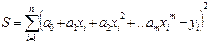(19)

Тоді система рівнянь для визначення а₀, а₁, … , а_m з врахуванням (17) набере вигляду

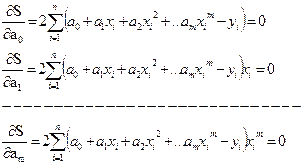(20)

Збираючи коефіцієнти при невідомих а₀, а₁, … , а_m, одержимо наступну систему рівнянь (16) перед знаком суми опускаєм − сталий множник, який не змінює коренів системи):

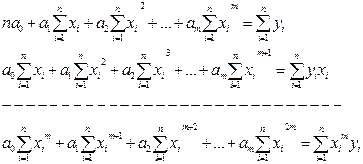(21)

Систему (21) можна записати в більш компактному вигляді:

с₀а₀ + с₁а₁ + с₂а₂ + … + с_ma_m = d₀ ,

c₁a₀ + c₂a₁ + c₃a₂ + … + c_m+1a_m = d₁ , (22)

– – – – – – – – – – – – – – – – – – – – – – – – – –

c_ma₀ + c_m+1a₁ + c_m+2a₂ + … + c_2ma_m = d_m ,

де

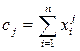,j = 0, 1, 2, … , 2m (23)

,k = 0, 1, 2, … , m (24)

Поліном (18) степені m < n, де n − число пар х_і, у_і забезпечує апроксимацію таблично заданої функції у_і(х_і) з мінімальною середньоквадратичною похибкою:

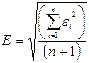
(25)

Якщо m = n, то має місце звичайна інтерполяція, тобто .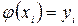

Зауваження : Система (22) − це система лінійних алгебраїчних рівнянь відносно невідомих а₀, а₁, … , а_m. Коефіцієнти при невідомих одержуються за формулами (23) та (24). Для обчислення і зберігання коефіцієнтів с_j потрібен масив із (2m+1) чисел, а для d_k − масив із (m + 1) чисел, де m − степінь полінома, яка задається на початку роботи програми.

Потрібно ввести в циклі (і=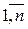) пари значень х_і, у_і, потім сформувати коефіцієнти при невідомих с_j та вільні члени d_k .

Одержану таким чином систему лінійних алгебраїчних рівнянь розв'язати методом Гауса (з частковим вибором головного елемента), одержуючи значення параметрів а₀, а₁, … , а_m апроксимуючого полінома φ(х).

На практиці використовується поліноміальна апроксимація за МНК з автоматичним вибором степені полінома. Алгоритм наступний: задається початкове значення m, потім шукається коефіцієнти полінома а₀, а₁, … , а_m , за формулою (25) обчислюється середньоквадратична похибка і порівнюється із заданою Е1. Якщо Е > заданої, степінь m збільшується на 1 і все повторюється. Обчислення припиняється при Е < E1.