Друга інтерполяційна формула Ньютона

Перша інтерполяційна формула Ньютона незручна для інтерполяції функції поблизу кінця таблиці. У цьому випадку використовується друга інтерполяційна формула Ньютона. Знайдемо цю формулу.

Нехай маємо систему значень функції

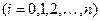
для рівновіддалених значень аргументу

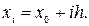
Побудуємо інтерполяційний поліном такого вигляду:

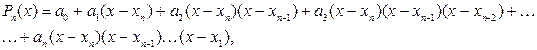
або, використавши узагальнений степінь, одержимо:

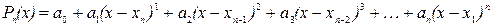(32)

Наше завдання полягає у визначенні коефіцієнтів а₀, а₁, а₂, а₃,…,а_n таким чином, щоб були справедливі рівності

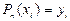
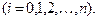
Для цього необхідно й достатньо, щоб

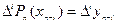
(33)

Покладемо х=х_n у формулі (14). Тоді будемо мати:

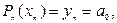
отже,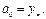

Далі беремо від лівої й правої частин формули (32) скінченні різниці першого порядку

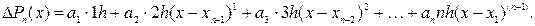
Звідси, поклавши х=х _n-1 і врахувавши співвідношення (33), будемо мати:

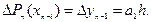
Отже,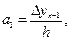

Аналогічно склавши другу різницю від 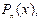одержимо:

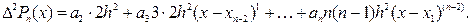
Поклавши х=х_n-2, знаходимо:

.

Отже,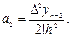

Характер закономірності коефіцієнтів 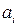зрозумілий. Застосувавши метод математичної індукції, можна довести, що

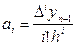
(34)

Підставляємо ці значення у формулу (30), будемо мати остаточно:

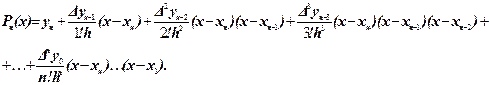(35)

Формула (35) називається другою інтерполяційною формулою Ньютона.

Введемо зручніший запис формули (35). Нехай , тоді

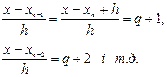
Підставимо ці значення у формулу (35), одержимо:

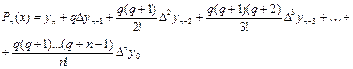(36)

Це і є звичайний вигляд другої інтерполяційної формули Ньютона. Для наближеного обчислення значень функції у покладають: 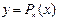.