Метод Рунге-Кутта другого порядку.
Для зменшення похибки методу інтегрування звичайних диференційних рівнянь, що використовує розкладання шуканого рішення в ряд Тейлора 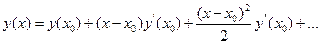 ,
,
необхідно враховувати більшу кількість членів ряду. Однак при цьому виникає необхідність апроксимації похідних від правих частин рівнянь. Основна ідея методів Рунге-Кутта полягає в тому, що похідні апроксимуються через значення функції 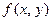 у вузлах на інтервалі
у вузлах на інтервалі  , що обираються з умови найбільшої близькості алгоритму до ряду Тейлора. В залежності від старшого степеня, з якого враховуються члени ряду, побудовані обчислювальні схеми Рунге-Кутта різних порядків точності.
, що обираються з умови найбільшої близькості алгоритму до ряду Тейлора. В залежності від старшого степеня, з якого враховуються члени ряду, побудовані обчислювальні схеми Рунге-Кутта різних порядків точності.
Для другого порядку отримано однопараметричне сімейство схем виду
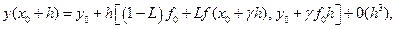 (37)
(37)
де 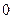 <
<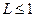 – вільний параметр,
– вільний параметр,
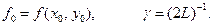
Локальна похибка схем (37) має третій порядок, глобальна - другий. Рішення рівняння, отримане за цією схемою, рівномірно сходиться до точного розв'язання з похибкою 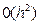 . Для параметра
. Для параметра  найбільш часто використовують значення
найбільш часто використовують значення 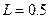 та
та  .
.
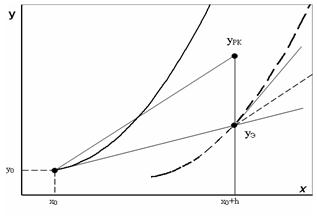
Рис. 12. Метод Рунге-Кутта другого порядку ( = 0,5)
= 0,5)
У першому випадку формула (37) приймає вигляд

геометрична інтерпретація якої представлена на рис. 12. Спочатку обчислюється наближене рішення рівняння в точці 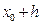 за формулою Ейлера
за формулою Ейлера 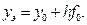 Потім визначається нахил інтегральної кривої у знайденій точці
Потім визначається нахил інтегральної кривої у знайденій точці 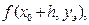 а після знаходження середнього нахилу на кроці
а після знаходження середнього нахилу на кроці  знаходиться уточнене значення
знаходиться уточнене значення 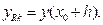 Схеми подібного типу називають «прогноз-корекція», що має на увазі грубе обчислення рішення за формулою низького порядку, а потім уточнення з урахуванням отриманої інформації про поведінку інтегральної кривої.
Схеми подібного типу називають «прогноз-корекція», що має на увазі грубе обчислення рішення за формулою низького порядку, а потім уточнення з урахуванням отриманої інформації про поведінку інтегральної кривої.
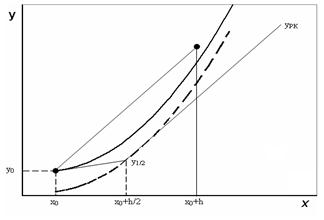
Рис. 13. Метод Рунге-Кутта другого порядку ( = 1)
= 1)
У другому випадку при  формула (37) приймає вигляд
формула (37) приймає вигляд
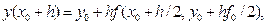
Геометричне значення якої відображено на рис. 13. При прогнозуванні визначається методом Ейлера значення в точці 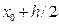

а після обрахування наклону дотичної до інтегральної кривої у середній точці рішення коректується з цього нахилу.