Метод прямокутників.

Метод прямокутників — найпростіший метод чисельного інтегрування, що полягає у заміні значень функції на проміжку значенням функції в деякій точці проміжку.

Види формули прямокутників:

1.1. Формула лівих прямокутників

В даному випадку береться значення функції на початку проміжку:

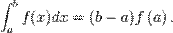
Похибка обчислення рівна: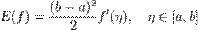

1.2. Формула правих прямокутників

В даному випадку береться значення функції в кінці проміжку:

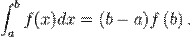
Як і впопередньому випадку похибка обчислень рівна: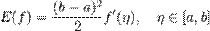

 

1.3. Формула центральних прямокутників

Дана формула має вид:

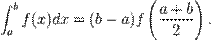
Похибка обчислень рівна: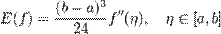

1.4. Великі формули прямокутників

Для збільшення точності обчислень проміжок інтегрування розбивається на дрібніші проміжки до кожного з яких застосовується формула прямокутників. Загалом кількість проміжків розбиття рівна n і Δ = (b − a) / n то велика формула прямокутників має вигляд:

де i' може бути рівним i − 1, i чи i − 1 / 2, що відповідає формулам лівих, правих і центральних прямокутників.

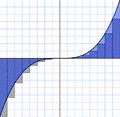
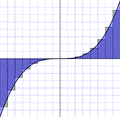
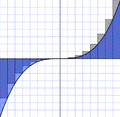
Рис. 13. Метод лівих Рис. 14. Метод центральних Рис. 15. Метод правих

прямокутників прямокутників прямокутників

 

Похибка великої формули центральних прямокутників задовольняє нерівність:

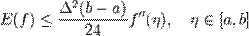
1. 2. Метод трапецій

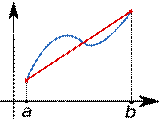
Рис. 16. Функція f(x) (синій колір) апроксимується

лінійною функцією (червоний колір).

Метод трапецій є методом наближеного обчислення значення визначеного інтегралу.

Ідея методу трапецій полягає в наближенні області під графіком функції f(x) трапецією та обчисленні її площі. Якщо застосувати цю ідею безпосередньо до інтервалу [a,b], то отримаємо

(39)

але це незадовільно з приводу великої похибки.

Для точнішого обчислення значення інтегралу, слід попередньо розбити інтервал інтегрування [a,b] на n підінтервалів 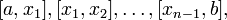та застосувати формулу (39) до кожного із них. Таким чином, отримуємо:

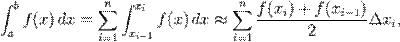
де Δx_i = x_i − x_{i − 1},x₀ = a,x_n = b.

У методі трапецій переважно застосується розбиття інтервалу інтегрування на n рівні відрізків довжиною h = Δx = (b − a) / n. Тоді попередня формула перетворюється на таку:

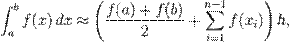(40)

і похибка, так званий залишковий член E(f) не перевищує за 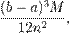де 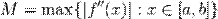— це максимум другої похідної функції f(x) на всьому інтервалі. Відзначимо, що за збільшення числа n інтервалів розбиття, залишковий член зменшується як O(1 / n²).

1. 3. Метод парабол (Сімпсона)

Метод Сімпсона є одним із методів чисельного інтегрування, названий на честь британського математика Томаса Симпсона (1710—1761)

Формулою Сімпсона називається інтеграл від інтерполяційного многочлена другого степеня на відрізку [a,b]:

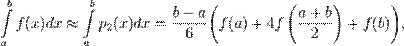(41)

де f(a), f((a + b) / 2) і f(b) — значення функції у відповідних точках .

При умові, що функція f(x) на відрізку [a,b] має похідну четвертого порядку, похибка E(f), дорівнює:

Зважаючи, що значення ζ переважно не є відомим, для оцінки похибки використовується нерівність:

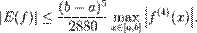
Для точнішого обчислення інтеграла проміжок [a,b] розбивається на N відрізків однакової довжини і застосовується формула Сімпсона на кожному з них. Значення інтеграла є сумою для всіх відрізків.

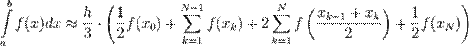(42)

де 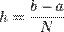величина кроку, а 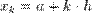межі відрізків.

Загальна похибка E(f) при інтегруванні на відрізку [a,b] з кроком x_i − x_{i − 1} = h визначається за формулою:

.

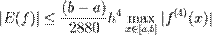При неможливості оцінити похибку за допомогою четвертої похідної можна використати слабшу оцінку:

.
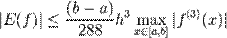