Тема 10. Дифференциальные уравнения
[2] гл. XXII § 1—13; [3] № 2058, 2067, 2094, 2102, 2165, 2186,2213,2215,
Разберите решение задач 12, 13 данного пособия.
Задача 12. Решить уравнение у'—уtgх =-у2соз х.
Решение. Данное уравнение является уравнением Бернулли. Для его решения (как и для линейного уравнения) искомую функцию у представим в виде произведения двух других функций: и=и(х) и 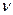 =
=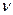 (x), то есть введем подстановку у=и*
(x), то есть введем подстановку у=и*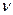 . Тогда у'=и'
. Тогда у'=и'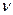 +и
+и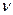 ' и данное уравнение примет вид:
' и данное уравнение примет вид:
и'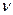 + и
+ и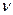 '- и
'- и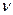 tg х= -
tg х= -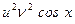 .
.
или
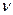 (и'-иtgх)+и
(и'-иtgх)+и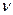 '=-
'=-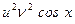 . (1)
. (1)
Выберем функцию и так, чтобы
и'-иtgх=0. (2)
При подобном выборе функции и уравнение (1) примет вид
и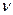 '=-
'=-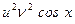 или
или 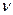 '=-
'=-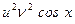 . (3)
. (3)
Решая (2) как уравнение с разделяющимися переменными, имеем:
 ,
, 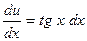 , In и = - In cos х, и=-
, In и = - In cos х, и=- .
.
Здесь произвольная постоянная С=0. Подставляя найденное значение и в уравнение (3) , имеем:
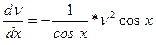 ,
,  ,
,  ,
, 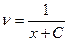 .
.
Тогда у=и*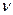 =
=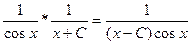 - общее решение данного уравнения.
- общее решение данного уравнения.
Задача 13. Найти частное решение уравнения у"+4у=4sin2х-8cos2х, удовлетворяющее начальным условиям у(0)=0, у' (0) =0.
Решение. Общее решение у данного уравнения равно сумме общего решения у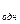 однородного уравнения и какого-либо частного решения у данного уравнения, то есть
однородного уравнения и какого-либо частного решения у данного уравнения, то есть
у= у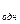 +
+ .
.
Для нахождения у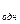 составим характеристическое уравнение R
составим характеристическое уравнение R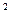 +4=0, имеющее комплексные корни.
+4=0, имеющее комплексные корни.
R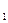 =2i и R
=2i и R =-2i. В этом случае общее решение однородного уравнения ищем в виде
=-2i. В этом случае общее решение однородного уравнения ищем в виде
у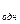 = е
= е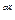 (С
(С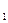 cos
cos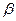 х+С
х+С sin
sin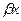 ), (4)
), (4)
где 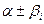 — комплексные корни характеристического уравнения. Подставив в (4)
— комплексные корни характеристического уравнения. Подставив в (4) 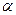 =0,
=0, 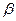 = 2, имеем:
= 2, имеем:
у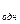 =C
=C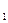 cos2х+С
cos2х+С sin2х.
sin2х.
Для нахождения частного решения  неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция f(х)= е
неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция f(х)= е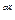 (аcos
(аcos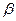 х+bsin
х+bsin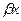 ) и числа
) и числа 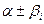 не являются корнями характеристического уравнения, то существует частное решение
не являются корнями характеристического уравнения, то существует частное решение
 = е
= е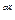 (Аcos
(Аcos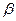 х+Вsin
х+Вsin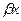 ). Если же числа
). Если же числа 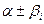 являются корнями характеристического уравнения, то существует частное решение
являются корнями характеристического уравнения, то существует частное решение
 = хе
= хе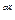 (Аcos
(Аcos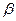 х+Вsin
х+Вsin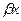 ).
).
Применяя эту теорему при 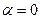 ,
, 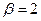 , имеем:
, имеем:
 = х (Аcos2х+Вsin2х).
= х (Аcos2х+Вsin2х).
Дважды дифференцируя последнее равенство, находим 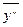 =(4В-4Ах)cos2х+(-4А-4Вх)sin2х.
=(4В-4Ах)cos2х+(-4А-4Вх)sin2х.
Подставив в данное уравнение  и
и 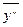 получим:
получим:
4Всоз2х—4Аsin2х=4sin2х-8соз2х,
откуда А =-1, В = —2.
Следовательно,  =-х(cos2х+2sin2х) и у= C
=-х(cos2х+2sin2х) и у= C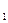 cos2х+С
cos2х+С sin2х-х(cos2х+2sin2х).
sin2х-х(cos2х+2sin2х).
Найдем у':
у'=-2 sin2х+2С cos2х- cos2х-2 sin2х-х(-2 sin2х+4 cos2х).
cos2х- cos2х-2 sin2х-х(-2 sin2х+4 cos2х).
Используя начальные условия, получим систему
 , откуда C
, откуда C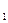 =0, С
=0, С =
=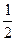 .
.
Следовательно,
у=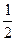 sin2х-х(cos2х+2sin2х) - есть искомое частное решение данного дифференциального уравнения.
sin2х-х(cos2х+2sin2х) - есть искомое частное решение данного дифференциального уравнения.