Тема II. РЯДЫ

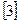гл. XX1 § 1 — 14: № 2424, 2426, 2474, 2475, 2503, 2519. 2533.

Разберите решение задач 14, 15 данного пособия.

Задача 14. Написать первые три члена ряда

найти интервал сходимости ряда и исследовать его сходи­мость на концах интервала.

Решение. Беря последовательно m=1, 2, 3, ..., запишем данный ряд в виде:

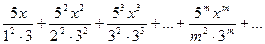
Для нахождения области сходимости ряда применим признак Даламбера

.

 

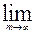
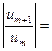
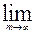
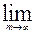
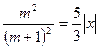Данный ряд сходится абсолютно при тех значениях х, которые удовлетворяют неравенству

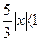, или , или -.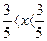

Исследуем сходимость ряда на концах полученного интервала.

При х=-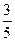'--данный ряд принимает вид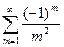

Последний ряд является знакочередующимся; абсолютная величина его общего члена стремится к нулю при m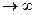. Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит,

х=-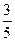принадлежит области сходимости данного ряда.

При х=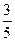данный ряд принимает вид .

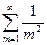Исследуем сходимость этого ряда при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл

=.

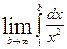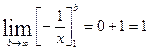Так как несобственный интеграл сходится, то сходится и исследуемый ряд. Значит, при х= 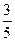исходный ряд сходится.

 

Таким образом, -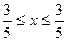область сходимости данного ряда.

 

Задача 15. Вычислить с точностью до 0,001.

Решение. Представим подынтегральную функцию в виде степенного ряда. Заменив х в разложении функции sinх на 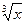, имеем:

sin =-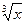

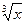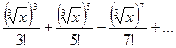
Тогда

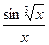=х-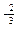

==

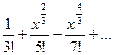
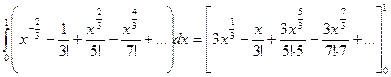=3-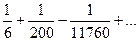

 

Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Так как четвертым его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена. Тогда

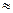3-