Упругость. Тензоры четвертого ранга

1. Закон Гука.

Под действием напряжения форма твердого тела изменится. Если величина напряжения ниже определенного предельного значения, называемого пределом упругости, то деформация является обратимой, т. е. при снятии напряжения тело принимает первоначальную форму.

Известно, что при достаточно малых напряжениях деформация пропорциональна величине приложенного напряжения.

Закон Гука:

,

где S – константа упругой податливости, или податливость, для конкретной системы напряжений и данного направления деформаций. В то же время можно записать

, ,

где С – константа упругой жесткости, или жесткость – модуль Юнга.

Однородное напряжение и однородная деформация определяются тензорами второго ранга. Если к кристаллу приложено произвольное однородное напряжение 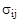, то возникающая однородная деформация такова, что каждая ее компонента линейно связана со всеми компонентами напряжения.

Для других восьми компонент имеются восемь аналогичных уравнений, где S – константы.

Закон Гука в обобщенной форме запишется

,

где 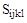– податливость кристалла (81 коэффициент).

Если приложена только одна компонента напряжения , то могут быть отличны от нуля все компоненты деформации, а не только .

А именно, если прямоугольный стержень, вырезанный из кристалла, подвергнуть одноосному растяжению параллельно четырем его ребрам, то стержень будет не только удлиняться в направлении растяжения, но и претерпевать сдвиг. При этом все углы между ребрами изменяются.

Если изгибать кристаллический стержень, прикладывая чисто изгибающее напряжение к его концам, то стержень будет не только изгибаться, но и закручиваться, и т.д.

Если уравнения решить как систему совместных уравнений относительно 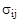, то получится система решений в форме

.

Физический смысл 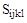можно понять, представив себе, что на кристалл действуют различные простые напряжения. Если бы было приложено сдвиговое напряжение 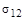, то, вспоминая, что в отсутствие объемных моментов 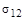не может быть приложено без , мы получили бы

.

Коэффициенты 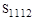и всегда появляются вместе. Если не принимать во внимание объемные моменты, то невозможно представить себе эксперимент, при котором можно было бы отделить 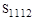от , или в более общем случае .

Поэтому, чтобы избежать появления произвольных постоянных, считают равными две компоненты:

.

Вместе с тем, если бы было приложено одноосное растягивающее напряжение параллельно Ох₃ (), то компоненты деформации задавались бы в виде:

;

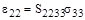и т.д.,

и .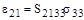

Но из определения тензора деформации мы видели 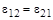, поэтому и в общем виде

.

Благодаря этому соотношению только 36 из 81 компонент 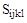являются независимыми.

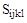образуют тензор четвертого ранга

Докажем это.

Мы имеем:

;

;

.

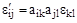Эти три уравнения связаны следующим образом:

;

;

,

поэтому, сравнивая коэффициенты, находим

.

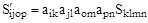Заменяя индексы суммирования, получим

,

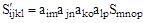а это есть закон преобразования тензора четвертого ранга.

Это уравнение соответствует 3⁴ уравнениям с 3⁴ членами с краевой стороны.

Благодаря симметричност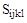и и по первым двум и по последним двум индексам, мы можем использовать матричные обозначения

.

В 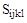два первых индекса объединяют в один, и два последних объединяют в один и вводят множители 2 и 4 следующим образом:

.

Тогда выражение

будет записано в матричном обозначении

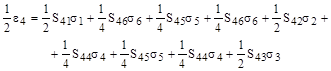
или

; .

Множители 2 и 4 вводятся в определение потому, что таким путем удается избежать появления этих множителей в уравнении и его можно записать в компактной форме. Таблицы для образуют матрицы. Для множители 2 и 4 вводить не нужно,

; ,

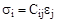это можно показать, но не будем здесь это рассматривать.