Физические уравнения
Физические уравнения для шарнирно-стержневой системы устанавливают взаимосвязь между удлинениями стержней и внутренними усилиями. Для линейно упругого материала физические уравнения имеют форму линейных алгебраических уравнений и основываются на законе Гука s = Еe, где s - нормальное напряжение при одноосном растяжении (сжатии), Е - модуль Юнга, e - относительная линейная деформация. Умножая записанное равенство на площадь F поперечного сечения стержня и учитывая, что e = 
, получаем:
, (5)
где константу k можно назвать коэффициентом жесткости стержня.
Запишем уравнение (5) для каждого стержня:
N1 = k1 D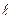
1, N2 = k2 D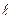2, …, Nm = km D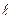m.
Объединение m равенств в одно векторное уравнение дает физическое уравнение
N =
d, (6)
в котором матрица называется матрицей «внутренней» жесткости системы; она имеет диагональный вид:
, 
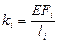(i = 1, 2, …, m). (7)
Уравнение (6) может быть записано в обратной форме d =
N,
где матрица обратна матрице (=
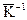) и называется матрицей «внутренней» податливости системы:
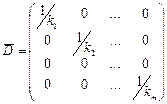. (8)
7 Полная система уравнений и методы её решения
Полная система уравнений состоит из уравнений равновесия узлов, геометрического и физического уравнений. Запишем физическое уравнение первым:
Объединим три уравнения в одно с вектором неизвестных [d,q,N]:
. (9)
Получили уравнение с симметричной матрицей порядка 2m + n. Порядок полной системы можно понизить, исключая вектор деформаций d из первого уравнения с помощью геометрического (третьего) уравнения. В результате получим систему с неизвестными векторами перемещений q и усилий N:
(10)
Матрица системы (10) имеет порядок m + n.
Формирование и решение систем (9) или (10) составляет суть смешанного метода. В этих системах в качестве неизвестных фигурируют векторы, имеющие различный физический смысл.
Исключение неизвестных можно продолжить. Если в качестве основных неизвестных принять вектор усилий N и из системы (10) исключить вектор перемещений q, то такой способ решения полной системы уравнений называется методом сил. Если же, наоборот, за вектор основных неизвестных принять вектор перемещений q, а из системы (10) исключить вектор усилий N, то такой способ решения полной системы называется методом перемещений.
Аналогами методов сил и перемещений в теории упругости являются решения задач в напряжениях и в перемещениях.
Наиболее просто получается разрешающее уравнение метода перемещений. Выразим вектор N из первого уравнения системы (10) и подставим его выражение во второе уравнение:
Kq = p. (11)
Матрица уравнения (11) является квадратной порядка n и определяется по формуле
. (12)
Матрицу К называют матрицей “внешней” жёсткости системы, или просто матрицей жёсткости системы (МЖС).
Следует особо отметить, что в случае геометрически изменяемых систем, а также систем с недостаточным числом опорных связей, ранг матрицы А меньше n, что приводит к вырожденности матрицы К и невозможности однозначного определения перемещений из уравнения (11). В дальнейшем будем считать, что такой ситуации не возникает. Решая уравнение (11), получаем вектор узловых перемещений q. Затем, используя геометрическое уравнение (3), находим вектор деформаций d и, наконец, с помощью физического уравнения (6) определяем вектор внутренних усилий N.
Уравнение (11) позволяет получить явную зависимость узловых перемещений от внешней нагрузки:
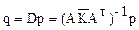. (13)
Матрица D обратна матрице К (D = K-1) и называется матрицей влияния перемещений; её также называют матрицей “внешней” податливости системы. Элемент 
матрицы D представляет собой перемещение узла системы по направлению qi от единичной силы, приложенной в узле по направлению qj .
С помощью уравнений (10) и (13) нетрудно получить явную зависимость внутренних усилий от внешней нагрузки:
.
Матрица 
называется матрицей влияния усилий.
Для статически определимых геометрически неизменяемых систем, для которых А является квадратной невырожденной матрицей, выражение для матрицы влияния усилий упрощается:
.
Опорные реакции определяются по уравнению (2) и могут быть выражены через нагрузку: r = RN = RZp.
Матрица Zr = RZ называется матрицей влияния опорных реакций.