РАСЧЕТЫ НА УДАР
Под ударом понимается взаимодействие движущихся тел в результате их'соприкосновения, связанное с резким изменением скоростей точек этих тел за весьма малый промежуток времени.
Время удараизмеряется в тысячных, а иногда и миллионных долях секунды, а сила удара достигает большой величины, например, действие кузнечного молота на кусок металла, удар падающего груза при забивке свай, воздействие колеса паровоза на рельс при перекатывании через стык идр.

|
На рис. 401 показан график изменения силы удара падающего груза в зависимости от времени. В точке С диаграммы сила удара достигает наибольшего значения. Вертикаль, проведенная через точку С, разде- Р ляет диаграмму на две части, соответствующие первой и второй фазам удара *.
Импульс силы удара
равен изменению количества движения ипоэтому может быть найденс достаточно высокой точностью; что же касается наибольшей силы удара /Jmax и его продолжительности т, то вопрос о достаточно точном определении этих величин до сего времени не может считаться разрешенным до конца. Объясняется это тем, что за исключительно короткий промежуток времени, в который совершается удар, трудно произвести какие-либо измерения, связанные с определением силы удара.
При ударе падающего груза по упругому стержню точка, по которой происходит удар, приобретаетнекоторую скорость движения; однако для развития деформаций всего стержня требуется время, которое может оказаться большим продолжительности удара т. Поэтому обычно производят условный расчет на удар, по которому определяют внутренние силы и перемещения, возникающие в стержне после удара в результате того, что падающее тело сообщило определенной точке начальную скорость движения. Так, например, определяется наибольшее динамическое перемещение точки, по которой наносится удар. Зная это перемещение, можно решать задачу об определении напряженного состояния стержня. В рамках определенных предположении
 * Различаютдве фазыудара. В первойфазе центры тяжести соударяемыхтел сближаются а сила взаимодействия между телами возрастает,достигая максимального значения вмомент наибольшегосближения тел, когда скоростьотносительного движения обращается в нуль.
* Различаютдве фазыудара. В первойфазе центры тяжести соударяемыхтел сближаются а сила взаимодействия между телами возрастает,достигая максимального значения вмомент наибольшегосближения тел, когда скоростьотносительного движения обращается в нуль.
Во второй фазе(фазе восстановления)центры тяжести тел удаляются друг oi друга силы взаимодействияуменьшаются, обращаясь внуль, вконце удара, когда прекращается контакт тел, или впостоянную величину, ранную весупадающего груз;,, если удар является абсолютно неупругнм.
можно найти силу, статически прикладываемую в точке удара, чтобы вызвать наибольшее динамическое перемещение системы. Такую силу условно называют динамической силой и обозначают РЛ*.
Рассмотрим случай, когда падающее тело весом G ударяет по другому телу весом Go, закрепленному на невесомой упругой пружине (рис. 402, а). Удар считаем абсолютно неупругим. Обозначим жесткость

|
пружины (силу, вызывающую смещение верхнего конца пружины на единицу) через с. Эту величину легко определить аналитически или экспериментально.
Если силу G приложить к системе статически, то перемещение Яст будет определяться равенством
После удара вследствие полученной начальной скорости пружина сожмется на величину Хд (рис. 402, б), которую можно определить через динамическую силу Рл:
К = Р*1с- (б)
Скорость падения груза в момент, предшествующий удару, связана с высотой падения равенством
V2 = 2gh. (в)
После соприкосновения двух тел их скорости одинаковы и равны У]. Таким образом, предполагаем, что после соприкосновения два тела как бы соединились в одно, которое, продолжая перемещаться вниз, сжимает пружину.
Предположим, что продолжительность удара т настолько мала, что груз Go, получив скорость Vx, начал вместе с грузом G сжимать пружину только после того, как закончился удар. Тогда по теореме об изменении количества движения имеем
следовательно,
При дальнейшем движении пружина сжимается, а скорость тел постепенно падает. В момент наибольшего сжатия сила, сжимающая пружину, достигнет максимума: РЛ + Go.
 * Такой расчет справедлив, когда масса падающего груза значительно больше массы стержня.
* Такой расчет справедлив, когда масса падающего груза значительно больше массы стержня.
Воспользуемся теоремой об изменении кинетической энергий согпасно к^орой приращение кинетической энергии материальной системы за ^который промежуток времени равно сумме работ, приложенных к системе сил на соответствующем пути:
оПРГЬ т - кинетическая энергия в момент наибольшего сжатия ЗА ' пружины. Так как в этот момент скорость равна нулю, то
Tl- кинетическая энергия после удара в "7Г!ГлеТяется движения, которая с учетом равенства (г) определяется
tit inOM/OUHPU
А - работа всех сил, приложенных к двум движущимся телам
на пути Хл. Сила тяжести двух тел на пути лд совершит работу

|
Со стороны пружины на тела действует переменная сила. В начале де^ршц™ пружины она равна силе веса 0„ а в конце - силе Go +РЖ. График изменения силы показан на рис. 41М. Работа этой силы будет отрицательной, так как она действует в сторону, противоположную движению. Численно работа равна площади диаграммы, показанной на рис. 403.
Таким образом, учитывая равенство (о), найдем
Подставляя найденные значения в равенство (д), получим
С учетом равенств (а) и (в) имеем
Решая это уравнение, найдем
где
Полученное решение является приближенным, так как при выводе формулы (17.2) не был учтен целый ряд факторов, а именно: удар считался абсолютно неупругим, в действительности в реальной системе он является частично неупругим.В то же время не были учтены местные деформации в точке, по которой наносится удар. Учет местных деформацийможет оказать существенное влияние на окончательный результат. Из-за сделанных отступлений от реальных условий формула (17.2) дает завышенное значение динамического перемещения.
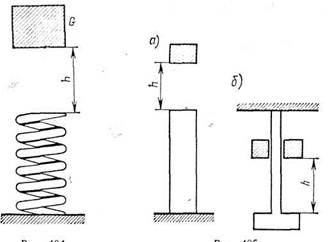
Если Со = 0, т. е. тело G падает на невесомую пружину (рис. 404), то динамическое перемещение идинамический коэффициент равны:
Формулу (17.4) можно применить к определению динамического коэффициента для невесомого стержня, т. е. для стержня, массой которого можно пренебречь по сравнению с массой падающего груза. При продольном ударе, вызывающем сжатие (рис. 405, а) пли растяжение (рис. 405, б) стержня, величину к необходимо заменить удлинением стержня А /:
Силу сжатия, а также соответствующие напряжения можно определить с помощью того же динамического коэффициента;
Чем больше статическое удлинение Л /С1, тем меньше динамический коэффициент. Таким образом, чем больше жесткость стержня, тем больше величина ударной силы.
Уменьшить силу удара можно, увеличив Д/С1 — статическое удлинение. Чем больше длина стержня и меньше его жесткость, тем меньше динамический коэффициент, а следовательно, меньше динамическая сила и динамические напряжения. Этим можно объяснить то, что при буксировке тяжелых барж канаты, соединяющие буксирный катер с баржей, имеют большую длину. Короткие канаты при случайном ударе, возникающем вследствие различных причин (например, когда баржа сядет на мель), не выдерживают динамической нагрузки и разрываются.
Если на стержень при продольном ударе поставить дополнительно пружину, то величина Л /ст значительно увеличится, а следовательно, уменьшится динамический коэффициент. Установка резиновых прокладок между машиной и фундаментом также уменьшает ударное воздействие.


При поперечном ударе (рис. 406) также можно пользоваться формулой (17.4), где величина к„ должна быть заменена величиной статического прогиба. Обозначим статический прогиб в точке падения груза через бст, тогда
 Величины динамического прогиба бд в произвольном сечении, динамического напряжения или какого-либо другого фактора Sa легко определяются с помощью динамического коэффициента:
Величины динамического прогиба бд в произвольном сечении, динамического напряжения или какого-либо другого фактора Sa легко определяются с помощью динамического коэффициента:
бд = цбст;
Величину динамического коэффициента при падении груза на невесомую балку можно выразить через скорость падения груза в момент подлета к балке. Для этого необходимо вместо величины 2Л подставить величину v2/g, что вытекает из формулы (в). Следовательно,
Когда высота падения равна нулю, динамический коэффициент равен двум. Такое загружение называется внезапным. Физически эту задачу можно представить так: если па нити подвесить груз, укрепив его над балкой таким образом, чтобы он касался верха балки, по не
■J4 Смирнов
давил на нее, а передавался целиком на нить, и если при этом нить мгновенно рассечь, то сила тяжести груза всей своей величиной внезапно передастся на балку. Напряжения и прогибы в этом случае будут в два раза больше, чем при статическом нагружении, при котором, как известно, предполагается постепенное нарастание величины нагрузки от нуля до конечного значения.
Если высота падения значительно превышает статический прогиб бст, то единицей по сравнению со вторым членом, стоящим под корнем, можно пренебречь. Тогда
Формулы (17.2) и (17.3) можно применить также к случаю, когда на невесомом стержне в точке падения груза весом G прикреплено тело весом Go (рис. 407).
Если груз падает на балку, обладающую значительной массой, которой нельзя пренебрегать, то решение сильно усложняется. Можнс применить приближенное решение; оно сводится к замене реальной балки системой с одной степенью свободы. Распределенная по длине балки масса заменяется приведенной массой, сосредоточенной в месте удара.
В формуле (17.3) содержатся не массы, а пропорциональные им веса соударяющихся тел. Если вес балки обозначить Qo, а вес приведенной массы — kQ, где к — коэффициент приведения (к < 1), то. подставляя в формулу динамического коэффициента (17.3) вместо G, величину kQ0, получим
Величина к зависит от способов закрепления стержня и вида ударг (продольный или поперечный удар).
Для определения величины к применяют приближенный прием. Для этого определяют кинетическую энергию заданной системы и срав нивают ее с кинетической энергией приведенной массы.
Рассмотрим частные случаи.
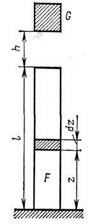
Продольный удар. Найдем величину для случая продоль ного удара по стержню постоянного сечения, заделанного однш концом (рис. 408). Пусть при ударе бесконечно малый элемент брусг с площадью поперечного сечения F и плотностью материала р, имею щий массу Fdzp, получил скорость V г. Предположим, что скоросп Vг пропорциональна перемещению заданного сечения, которое в свок очередь пропорционально величине г, т. е. эпюра динамических пере мещений по форме такая же, как от статической продольной силы приложенной на конце стержня. Тогда закон изменения скорости m высоте бруса может быть представлен в виде
v —JLv
v г — ^ ' >
где V — скорость верхней точки стержня. 418
Кинетическая энергия стержня равна
Таким образом, для стержня, заделанного одним концом, обладающего весом Qo = Flpg, коэффициент приведения при продольном ударе к = 1/3.
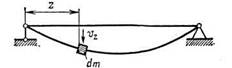
Поперечный удар. Рассмотрим балку постоянного сечения, шарнирно закрепленную на двух опорах. Для определения кинетической энергии системы предположим, что скорость Уг элемента балки, отстоящего от левой опоры на расстоянии г (рис. 409), пропорциональна перемещению этого сечения vz от статической нагрузки, приложенной в виде силы Р в точке удара. Это условие пропорциональности можно выразить следующим равенством:
Здесь УтЯх и i>raax — соответственно скорость и прогиб в середине пролета.
Приняв, что точка удара расположена в середине балки, имеем следующее уравнение прогибов:
Следовательно,
Кинетическая энергия системы определяется равенством
 Найдем теперь кинетическую энергию для балки, у которой посередине пролета приклеплена приведенная масса. Считая, что скорость
Найдем теперь кинетическую энергию для балки, у которой посередине пролета приклеплена приведенная масса. Считая, что скорость
14*
движения этой массы будет равна величине VmaK, получим
Две системы можно считать эквивалентными друг другу, если у них кинетические энергии одинаковы. Если приравнять два полученных выше выражения для энергий, то легко заметить, что коэффициент к определяется равенством
к =17/35.
Подставив найденное значение к в формулу (17.3'), определим для балки на двух опорах при ударе падающим грузом в точку, расположенную посередине пролета, значение динамического коэффициента:
где Qo — вес балки;
G — вес падающего груза; h — высота падения;
бст — прогиб балки в точке удара от статического действия груза.

Рассмотрим примеры, поясняющие применение полученных результатов.
Пример 1. Определить наибольшее динамическое напряжение в деревянном брусе переменного сечения, показанном на рис. 410, от удара, возникшего в результате падения груза весом Q = 100кх с

высоты 9 см. Модуль упругости древесины Е = 105 /сгс'сл<2. Все размеры показаны па рисунке.
Предположив, что груз приложен статически, найдем укорочение стержня:
Подставляя полученное значение статического перемещения в формулу динамического коэффициента, найдем
Статическое напряжение в нижней части стержня равпч
ост = 100/50 = 1 кгс/см-.
Динамическое напряжение определяется равенством од= ца„ = 2 • 101 =202 кгс/см-.
Полученные динамические напряжения довольно значительны. В действительности в деревянном брусе напряжения будут меньше. Объясняется это рядом причин: одна из них заключается в том, что при ударе появятся местные деформации, которые поглотят часть кинетической энергии.
Пример 2. На балочную систему, показанную на рис. 411, в точку К падает груз с высоты h. Определить динамический момент в заделке и динамические прогибы в точках В и К. Размеры балки и жесткости ее элементов показаны на рисунке.
В первую очередь находим статический прогиб точки К в месте падения груза. Его можно определить как сумму двух перемещении, а именно: 1) считая балку ВС недеформируемой, найдем перемещение точки К как половину прогиба в точке В; 2) считая консоль недеформируемой, найдем прогиб точки К в балке ВС.
Первое перемещение определяется выражением
Второй прогиб равен величине
Суммарный статический прогиб в точке К равен
Динамический коэффициент определим по формуле (17.4):
Далее легко найти требуемые (по условию задачи) величины: динамический момент в заделке
динамический прогиб в точке В
динамический пгюгиб в точке К
Здесь следует обратить особое внимание на то, что во всех случаях берется один и тот же динамический коэффициент. При определении последнего статический прогиб берется в той точке, по которой производится удар.