ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГОЙ СИСТЕМЫ
Если на систему действует сила Р (/), изменяющаяся во времени по какому-либо закону, то колебания балки, вызванные действием этой силы, называют вынужденными. После приложения силы инерции балку в отклоненном состоянии можно рассматривать как находящуюся в равновесии (рис. 419). Перемещение % теперь уже нужно определить от двух сил — i и Р (/):
i = bn[i+p(t)i
где бп — прогиб от единичной силы, приложенной в месте прикрепленной массы.
Заменяя силу инерции ее значением и перенося неизвестные в левую часть, после деления всех членов на т8п получим
§ + 4>% = LP(t). (17.16)
Интеграл этого уравнения состоит из двух частей: решения однородного уравнения и частного интеграла, зависящего от вида правой части.
Рассмотрим частный случай, когда внешняя сила представляет собой вибрационную (периодическую) нагрузку, меняющуюся по гармоническому закону с частотой б,
Р (t) = P sin et, 428-
то получим

|
Первое слагаемое этого выражения представляет собой собственные колебания, а второе описывает вынужденные колебания. Величины А и v определяют из началь-ных условий.
Так как собственные
колебания в реальных бал-
ках быстро затухают, то
рассмотрим только вынуж-
денные колебания, которые
происходят с частотой 8. ис'
Наибольшее отклонение стержня от своего первоначального положения (т. е. амплитуда вынужденных колебаний) будет найдено, если принять sin 8 = 1:
t __Jki_ _t ..
Smax — q,, — -CTJ1.
Для исследования значения динамического коэффициента
приведен график на рис. 420 абсолютного значения величины ц.
Из этого графика видно, что в том случае, когда частота вынужденных
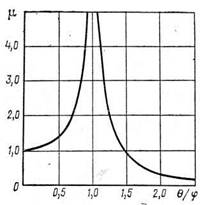
|
колебаний 0 приближается к частоте собственных колебаний <р, динамический коэффициент }х безгранично возрастает (при 0 = ф ц ->- оо). Такое явление называется резонансом.
Если учесть затухание (силы внутреннего сопротивления), то вместо уравнения (17.16) получим следующее дифференциальное уравнение:
Уравнение вынужденных колебаний (17.20) отличается от уравнения собственных колебаний (17.12) не только наличием правой части, но
и коэффициентом при первой производной -4. Вместо величины 2р
введенной в уравнение (17.12), принят коэффициент 2рх.
Как уже говорилось в предыдущем параграфе, гипотеза Фойгта не может быть безоговорочно принята при изучении колебаний упругих систем. Ее можно использовать при условии, что величина к в формуле (17.11) не является постоянной, а зависит от частоты колебаний. Результаты теории и опыта будут в большей мере согласованы, если
принять, что при собственных колебаниях х = хф = ^-, а при установившихся вынужденных колебаниях, совершающихся с частотой 0, (Здесь у — логарифмический декремент затухания.)
Этим и объясняется то, что коэффициенты 2|3 и 2р в уравнениях (17.12) и (17.20), учитывающие влияние сил сопротивления, различны.
Отношение двух коэффициентов pV|3 будет такое же, как отношение
(17.21)
Частное решение уравнения (17.20), соответствующее чисто вынужденным колебаниям, может быть записано в виде
l = B1sinQt + B2coset. (17.22)
Подставляя это выражение в уравнение (17.20) и объединяя члены, содержащие sin 0/ и cos 0/, получим
Г(ф2 _ е^) вг - 2Pi0S2 - |-1 sin 0* + [2Pi0Bx + (Ф2 - ©2) Вг] cos 0/ = 0.
Это уравнение^ должно тождественно обращаться в нуль при любых значениях t. Данное условие будет выполняться, если коэффициенты при sin 0^ и cos 0/ приравнять нулю. В результате получим два уравнения с двумя неизвестными Вх и В2:
Решая полученные уравнения, найдем:
(17.23)