Плоская гармоническая волна
Пусть фронт плоской гармонической волны распространяется в направлении оси x. Обозначим через ξ смещение в момент времени  любой частицы относительно ее положения равновесия, которое задается координатой
любой частицы относительно ее положения равновесия, которое задается координатой 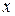 оси
оси 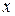 .
.
В этом случае волновые поверхности будут представлять плоскости, перпендикулярные к оси 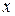 . Все частицы, имеющие одну и ту же координату
. Все частицы, имеющие одну и ту же координату 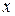 , но разные
, но разные  и
и  , будут принадлежать одной и той же волновой поверхности — плоскости x = const и колебаться одинаковым образом, т. е. ξ будет зависеть только от
, будут принадлежать одной и той же волновой поверхности — плоскости x = const и колебаться одинаковым образом, т. е. ξ будет зависеть только от 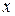 и
и  . В связи с этим поставленную задачу можно свести к рассмотрению колебаний частиц, положения равновесия которых лежат на оси
. В связи с этим поставленную задачу можно свести к рассмотрению колебаний частиц, положения равновесия которых лежат на оси 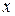 .
.
Если колебание частиц, лежащих в плоскости  , имеют вид
, имеют вид

то в плоскости, соответствующей произвольному значению 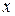 , колебания частиц будут отставать по времени на τ от колебаний частиц в плоскости
, колебания частиц будут отставать по времени на τ от колебаний частиц в плоскости  . Отставание связано с тем, что волна пройдет путь от плоскости
. Отставание связано с тем, что волна пройдет путь от плоскости  до плоскости
до плоскости  за время
за время 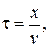 где v — скорость распространения волны. Можем написать
где v — скорость распространения волны. Можем написать
 (14.1)
(14.1)
Введем волновое число
 (14.2)
(14.2)
где λ — длина волны. С учетом формул (10.6) и (13 2) перепишем выражение (14.2) в виде
 (14.3)
(14.3)
С учетом соотношения (14.3) уравнение (14.1) примет вид
 (14.4)
(14.4)
Уравнение (14.4) является уравнением плоской гармонической волны, распространяющейся в направлении оси 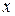 .Уравнение волны, распространяющейся противоположно направлению оси
.Уравнение волны, распространяющейся противоположно направлению оси 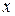 , отличается от уравнения (14.4) только знаком плюс при
, отличается от уравнения (14.4) только знаком плюс при  .
.
Уравнение (14.4) является решением дифференциального уравнения. Получим его. Для этого дважды продифференцируем ξ по 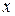 и
и  :
:

 (14.5)
(14.5)

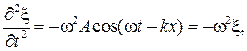
откуда
 (14.6)
(14.6)
Подставляя выражение (14.6) в соотношение (14.5), получаем

или, с учетом формулы (14.3), получаем окончательно
 (14.7)
(14.7)
Дифференциальное уравнение (14.7) называют волновым уравнением плоской гармонической волны, распространяющейся вдоль оси 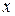 .
.