Распределение Пуассона.

В физике нередко приходится встречаться с измерениями, результаты которых пред­ставляются в виде небольших целых чисел. Через счетчик Гейгера за время измерения про­ходит не очень большое и при этом, конечно, целое число частиц. Делящееся ядро может распадаться на две, на три, или даже на четыре, но обязательно на целое и притом небольшое число частей. Статистические закономерности, которые имеют место в этом случае, несколько отличаются от изученных нами ранее; отличаются и правила вычисления ошибок.

Рассмотрим счетчик, регистрирующий космические частицы. Ясно, что число срабатываний счетчика за любой промежуток времени является целым числом. Однако интенсивность n космического излучения (т.е. число срабатываний счетчика в секунду, усредненное за очень большой - в пределе за бесконечный отрезок времени), вообще говоря, целым числом не выражается.

Найдем вероятность того, что при интенсивности n счетчик сработает за секунду n раз.

Поскольку мы переходим теперь к вычислению вероятностей, следует представить себе очень большое число совершенно одинаковых одновременно работающих счетчиков. Некоторая часть их сработает за секунду n раз. Доля, составляемая этими счетчиками по отношению к полному числу счетчиков, и равна вероятности того, что через счетчик за се­кунду пройдет ровно n частиц.

Обозначим полное число счетчиков буквой N. Через них в секунду в среднем прохо­дит Nn частиц, а за небольшое время dt пройдет Nndt частиц. Если dt достаточно мало, то ни через один из счетчиков за это время не пройдет двух частиц, и наши счетчики можно разбить на два класса: те, через которые за dt прошла одна частица, и те, через которые не про­шло ни одной. Последние составляют, конечно, огромное большинство. Число счетчиков, через ко­торые прошла одна частица, равно, очевидно, числу сосчитанных частиц Nndt, а их доля по от­ношению к полному числу счетчиков составляет

Nndt/N=ndt.

Вероятность того, что за время dt через счетчик пройдет одна частица, равна, следовательно, ndt. Это утверждение справедливо только для очень малого времени dt.

Вычислим теперь вероятность Po(t) того, что за время t через счетчик не пройдет ни одной частицы. По определению число таких счетчиков в момент t составляет NP_o(t), а в момент t+dt равно NP_o(t+dt). На основании предыдущего ясно, что из NP_o(t) счетчиков за время dt сработают NP_o(t)vdt. Поэтому

NP_o(t+dt)=NP_o(t)-NP_ondt,

или

P_o(t+dt) – P_o(t)= – P_ondt,

Интегрируя, найдем

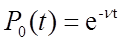(1).

При интегрировании было принято во внимание, что в начальный момент времени вероят­ность найти счетчик, не сработавший ни разу, равна единице.

Вычислим, теперь P_n(t+dt) - вероятность того, что за время t+dt через счетчик прой­дет ровно n частиц. Эти счетчики делятся на две категории. К первой принадлежат те, через которые все n частиц прошли за время t (а за время dt не прошло ни одной частицы). Ко второй принадлежат счетчики, через которые за время t прошло n-1 частиц, а последняя - за промежуток dt. Число первых равно NP_n(t)(l-ndt), а число вторых составляет NP_n-1(t)ndt.

Имеем, следовательно,

NP_n(t+dt)=NP_n(t)( 1-ndt)+ NP_n-1(t)ndt

Перенесем NP_n(t) влево и разделим обе части равенства на N×dt:

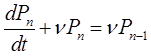(2)

Последовательно применяя рекуррентную формулу (2), с помощью (1) найдем

(3)

Заметим теперь, что nt, которое мы обозначим через n₀, равно среднему числу час­тиц, проходящих через счетчик за время t. Введя в (3) n_о, найдем

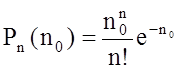(4)

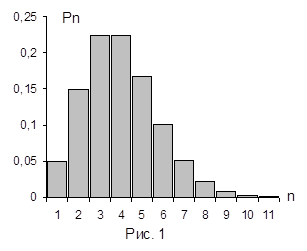
Формула (4) определяет закон распределения Пуассона. В ка­честве иллюстрации на Рис. 1 изображено распределение Пуассона для n₀=З. Ни для какого n величина P₀ не равна нулю. Она достигает макси­мума при n=3. Вероятность n=0 оказывается довольно велика. Достато­чно велика также веро­ятность того, что счетчик сработает не 3, а 6 или даже 8 раз.

Рассмотрим некоторые свойства формулы (4). Вычислим прежде всего вероятность найти ка­кое угодно значение n:

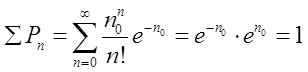
Этот результат является очевидным, поскольку мы вычисляли вероятность достоверного события. Вычислим среднее значение

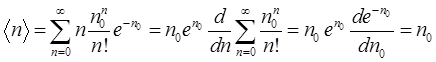(5).

Полученный результат также можно было без труда предсказать заранее.

Найдем теперь среднее квадратичное отклонение (стандартную ошибку):

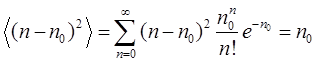(6)

(вычисление суммы в качестве полезного упражнения мы представляем читателю). Имеем, следовательно,

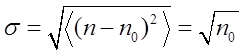(7).

Стандартная ошибка равна корню из среднего числа отсчетов.