Биномиальный закон распределения дискретной случайной величины
Определение: Биномиальным называется закон распределения дискретной случайной величины Х- числа появлений события А в n независимых повторных испытаниях, в каждом из которых события А может наступить с вероятностью p или не наступить с вероятностью q=1-p. Тогда Р(Х=m)-вероятность появления события А ровно m раз в n испытаниях вычисляется по формуле Бернулли:
Р(Х=m)=Сmnpmqn-m
Математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной по бинарному закону, находят, соответственно, по формулам:
M(X)=np,
D(X)=npq,
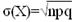
Если число испытаний n очень велико, а вероятность появления события А в каждом испытании очень мала (р≤0,1), то для вычисления Р(Х=m) используют формулу Пуассона:
Р(Х=m)=Рn(m)= e-λ • λm , где λ=np
m !
Тогда говорят, что случайная величина Х - распределена по закону Пуассона.
Так как вероятность р события А в каждом испытании мала, то закон распределения Пуассона называется законом средних явлений.
5. Непрерывная случайная величина.
Случайная величина Х наз. непрерывной, если ее значения заполняют конечный или бесконечный промежуток (а1;а2) числовой оси.
Функцией распределения(или интегральной функцией распределения) случайной величины Х наз. функция F(x), равная при каждом xͼR вероятности того, что X в результате испытания примет значение меньше X F(x)=P(X<x), xͼR.
Свойства функции распределения:
Знач. функции распред. принадлежит отрезку [0;1]; F(x)-неубывающая функция: если x2>x1 то F(x2)≥F(x1); вероятность попадания случайной величины X в один из промежутков (a;b), [а;b); (a;b] или [a;b] равна разности значений функции F(х) в точках b и a P(a<X<b)=P(a≤X<b)=P(a<X≤b)=P(a≤X≤b)=F(b)-F(a); вероятность того, что непрерывная случайная величина X примет одно определенное значение 0; F(-∞)=0, F(+∞)=1; если X- непрерывная случайная величина, то функция F(х) непрерывна на (-∞;+∞).
Плотностью распределения вероятностей(или дифференциальной функцией распред.) непрерывной случайной величины X наз. функция f(х)=F'(x), xͼR.
6. Числовые характеристики непрерывной случайной величины.
Математическим ожиданием М(Х) непрерывной случайной величины Х наз. число, вычисляемое по формуле: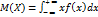 
При условии, что этот интеграл сходится.
Свойства математ. ожидания:1.М(С)=С, где С- постоянная величина; 2.М(СХ)=С*М(Х),где С- постоянная величина 3. М(Х1+Х2)=М(Х1)+М(Х2).
Дисперсией D(Х) непрерывной случайной величины Х наз. матем. ожид. квадрата отклонения случ. вел Х от ее матем. ожид, то есть D(X)=М(Х-М(Х))2 . Свойства дисперсии: D(C)=0, где с- постоянная величина; D(CX)=C2*D(X), где с-постоянная велечина; D(X1+X2)=D(X1)+D(X2);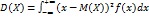 
, 
.
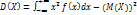Cреднее квадратическое отклонение непрерывной случайной величины Х: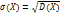 
.
7. Равномерный закон распределения непрерывной случайной величины.
Равномерным называется распределение такой случайной величины, все значение которой лежат на некотором интервале (a;b) и плотность распределения вероятностей задана формулой:
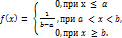
Функция распределения вероятностей такой случайной величины:
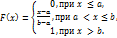
Числовые характеристики: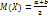 
, 
, 
.
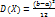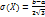8. Показательный закон распределения непрерывной случайной величины.
Показательным называется распределение такой случайной величины, у которой функция плотности распределения вероятностей задана формулой:
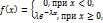где λ – некоторое положительное число.
Функция распределения F(x) таких случайных величин: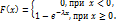 
Числовые характеристики: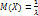 
, 
, 
.
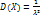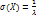9.Нормальный закон распределения НСВ; определение и его числовые характеристики М(х) м Д(х).
Нормальный закон распределения подчиняется непрерывной случайной величине у которой функция плотности распр. Вероятности:
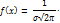
Параметрами нормального закона является числа m и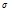
которые представляет собой 2 числовые характеристики этого закона
M(X)=m ; D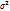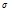(X)= 
;(X)=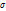 
Вероятность того , что случайная велечина Х примет значение из интервала ( a;b), вычисляется по формуле:
P(a<X<b)=Ф(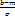
) – Ф(
)
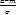Вероятность того , что абсолютная величнина отклонения Х от ее математического ожидания м меньше положительного числа.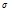
График функции плотности вероятности носит название норм. Кривая или кривая Гаусса