Измерение больших величин
Что такое большие и малые измеряемые величины? Рассмотрим этот вопрос на примере измерения электрического сопротивления с помощью моста постоянного тока.
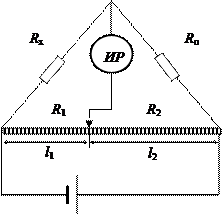 На рисунке ИР – индикатор равновесия, R0 – образцовое сопротивление, R1 и R2 сопротивления плеч реохорда, l1 и l2 – длины плеч реохорда.
На рисунке ИР – индикатор равновесия, R0 – образцовое сопротивление, R1 и R2 сопротивления плеч реохорда, l1 и l2 – длины плеч реохорда.
Условие равновесия моста в данном случае имеет вид 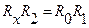 , откуда
, откуда  .(1). Очевидно, что
.(1). Очевидно, что 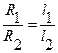 , (2), причем l1+l2=L=const. (3). Из (1) и (2) следует, что
, (2), причем l1+l2=L=const. (3). Из (1) и (2) следует, что  . Логарифмируя и дифференцируя это выражение, получим:
. Логарифмируя и дифференцируя это выражение, получим: 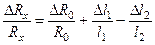 , где
, где  — погрешность оценки сопротивления Rx,
— погрешность оценки сопротивления Rx, 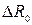 — погрешность образцового сопротивления R0,
— погрешность образцового сопротивления R0, 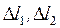 — погрешности измерения длины.
— погрешности измерения длины.
Из (3):  , и (4), найдём:
, и (4), найдём:  (5),
(5),  – относительная погрешность измерения.
– относительная погрешность измерения.
Очевидно  ,
,  . Можно записать (5) в виде:
. Можно записать (5) в виде:  . Учитывая, что L=l1+l2, после простого преобразования, получим
. Учитывая, что L=l1+l2, после простого преобразования, получим 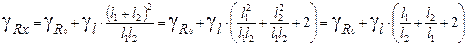 .
.
Из (1) и (2) следует, что  , из предыдущего выражения, получим
, из предыдущего выражения, получим
 (6)
(6)
Из (6) следует, что  как при Rx®0, так и при Rx®¥.
как при Rx®0, так и при Rx®¥.
Учитывая, что резистор R0 образцовый, его погрешностью 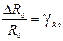 можно пренебречь. Тогда формула (6) запишется в виде
можно пренебречь. Тогда формула (6) запишется в виде 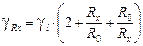 (7)
(7)
Эта формула позволяет вычислить относительную погрешность измерений как больших, так и малых величин.
Найдём вид полосы неопределённости. Поскольку, с учетом знаков абсолютной погрешности, сигнал на выходе нашего СИ, приведенный к входу, , вид полосы неопределенности определяется следующими соотношениями:
, вид полосы неопределенности определяется следующими соотношениями:  (8).
(8).
Поскольку абсолютная погрешность  , из формулы(7), пренебрегая величиной
, из формулы(7), пренебрегая величиной 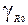 , имеем
, имеем  . (9). Учитывая (8), найдем максимальный и минимальный сигналы на выходе:
. (9). Учитывая (8), найдем максимальный и минимальный сигналы на выходе: 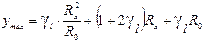 (10).
(10).
 Функция
Функция – парабола, ветви которой обращены вверх. В свою очередь,
– парабола, ветви которой обращены вверх. В свою очередь,  (11).Функция
(11).Функция – парабола с ветвями, обращенными вниз. На графике зависимости
– парабола с ветвями, обращенными вниз. На графике зависимости 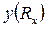 параметр d – ширина полосы неопределенности Rxмакс и Rxмин — максимальное и минимальное значения, которые еще могут быть измерены.
параметр d – ширина полосы неопределенности Rxмакс и Rxмин — максимальное и минимальное значения, которые еще могут быть измерены.
При Rx=Rxмакс и Rx=Rxмин погрешность DRx=DRx max=Rx, так что gRx=1 (или gRx=100%) и 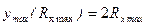 .
.
Ширина полосы неопределенности d определяется по формуле 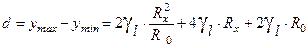 (12) Функция d(Rx) – парабола. Обозначим в формуле (7)
(12) Функция d(Rx) – парабола. Обозначим в формуле (7) 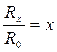 , тогда
, тогда 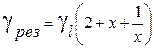 . Проведем анализ этой формулы. Сначала найдем минимум функции
. Проведем анализ этой формулы. Сначала найдем минимум функции  , взяв производную по х. Найдем, что при х=1
, взяв производную по х. Найдем, что при х=1 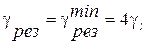 . Найдем максимально и минимально возможные значения х. Они находятся там, где
. Найдем максимально и минимально возможные значения х. Они находятся там, где 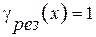 . Из этого равенства имеем
. Из этого равенства имеем 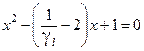 . Обычно
. Обычно  . Решая квадратное уравнение, получим
. Решая квадратное уравнение, получим  .
.
Т.к. при a<<1, где 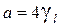 , выполняется соотношение
, выполняется соотношение 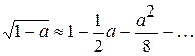 , получим:
, получим: . Отсюда следует, что
. Отсюда следует, что 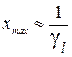 и
и 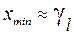 , где
, где  и
и  - погрешность реохорда. Отсюда легко найти минимальное и максимальное значения Rx, которые можно измерить с погрешностью £100%. Таким образом, значения
- погрешность реохорда. Отсюда легко найти минимальное и максимальное значения Rx, которые можно измерить с погрешностью £100%. Таким образом, значения  следует отнести к большим значениям, а значения
следует отнести к большим значениям, а значения 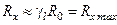 – к малым.
– к малым.
Значение 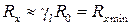 – это нижний порог чувствительности данного СИ, значение
– это нижний порог чувствительности данного СИ, значение 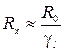 – это верхний порог чувствительности СИ.
– это верхний порог чувствительности СИ.
Обобщим полученные результаты. Пусть в формуле (7)  – любая величина, подлежащая измерению. Будим считать, что:
– любая величина, подлежащая измерению. Будим считать, что:
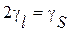 — погрешность чувствительности,
— погрешность чувствительности,
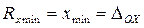 – нижний порог чувствительности,
– нижний порог чувствительности,
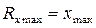 – верхний порог чувствительности,
– верхний порог чувствительности,
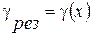 – погрешность СИ.
– погрешность СИ.
Подставляя эти обозначения в формулу (7): 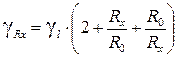 , получим универсальную формулу для расчета статических погрешностей СИ:
, получим универсальную формулу для расчета статических погрешностей СИ:
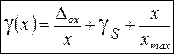 , (13), где
, (13), где  - абсолютная погрешность прибора (сдвиг нуля),
- абсолютная погрешность прибора (сдвиг нуля), 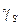 - погрешность чувствительности (погрешность наклона функции преобразования) или мультипликативная погрешность.
- погрешность чувствительности (погрешность наклона функции преобразования) или мультипликативная погрешность.