ОБЪЕМ ВЫБОРКИ N > 50
Выборкой большого объема будем считать выборку, в которой несколько значении переменных встречаются по 2 и более раза.
Пример. Определим коэффициент корреляции между случайными величинами размеров двух деталей, обрабатываемых одновременно на одном станке. После обработки, каждой пары деталей производятся измерения, результаты которых заносятся в протокол (см. табл. 15).
Таблица 15
| Номер опыта (№) | ... | ||||||||
| Деталь Х | 21,867 | 21,845 | 21,871 | 21,878 | 21,847 | 21,867 | 21,867 | ... | 21,867 |
| Деталь Y | 21,852 | 21,843 | 21,864 | 21,871 | 21,838 | 21,852 | 21,853 | ... | 21,854 |
В каждом ряду отыскиваются минимальные и максимальные значения (21,845 мм - 21,878 мм, 21,838 мм -21,871 мм). Если разность между этими значениями велика, то все значения целесообразно разбить на группы. В нашем примере 21,878-21,845=0,033мм и 21,871-21,838=0,033 мм. Объединим все значения в группы с шириной интервала h = 0,002 мм. Затем строим корреляционную таблицу (см. табл. 16), в которой приводятся интервалы, середины интервалов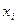 
и 
и значения новых случайных величин 
и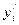 
, которые получаются по следующим формулам
; 
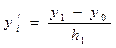, где 
-величины интервалов.
За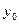 
и 
обычно принимают среднее значение середин интервалов. Примем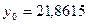 
; 
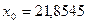. В рассматриваемом примере 
. Переход к новым случайным величинам целесообразно делать в тех случаях, когда середины интервалов 
; имеют двухзначные и более значения.
Для заполнения корреляционной таблицы пользуемся протоколом измерения деталей (табл. 15). Берем первый результат измерения 21,867-21,852. Ищем в табл. 16 по горизонтали интервал, содержащий число 21,867, а по вертикали-22,852. На пересечении этих координат ставим точку (обведена кружочком). Затем берем второй результат измерений 21,845-21,843, ищем интервал, содержащий эти значения, и на пересечении координат ставим точку (также обведена кружочком). Так поступаем со всеми парами замеров деталей.
В результате заполнения корреляционной таблицы получаем частоты встречаемости (
) всех различных пар значений . Затем приступаем к определению эмпирического значения коэффициента корреляции, обозначаемого через 
по формуле (d)
, (d)
где n-число опытов;
-частота совместного наступления событий Х и У.
Последовательность вычисления r приведена в строках 1-5 и колонках 1-3 табл. 16.
Значения 
находятся как суммы частот по всем колонкам и строкам.
Находим 
, как сумму значений 1-й строки (
) и 1-й колонки (
). Равенство и служит контролем правильности вычисления 
и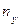 
.
Все значения умножаем на и записываем во 2-й строке. Суммируя все значения этой строки, получаем 
.
Все значения 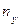умножаем на 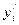записываем по 2-й колонке. Суммируя все значения этой колонки, определяем 
.
Находим произведения значений строки 1 на 
и заполняем 3-ю строку. Суммируя значения этой строки, получим, что 
.
| Корреляционная таблица | ||||||||||||||||||||||||||||
| Таблица 16 | ||||||||||||||||||||||||||||
| х'i | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | ||||||||||||||||||||
| Середина интервалов хi | 21,8385 | |||||||||||||||||||||||||||
| y'i | Середина | интервалов | уi | y x | 21,838-21,839 | 840 841 | 842 843 | 844 845 | 846 847 | 848 849 | 850 851 | 852 853 | 854 855 | 856 857 | 858 859 | 860 861 | 862 863 | 864 865 | 866 867 | 868 869 | 870 871 | ny' | ny' y' | ny' (y')2 | ||||
| -8 | 21, | 21,845-21,846 | 
| -16 | ||||||||||||||||||||||||
| -7 | 847 848 | 
| -7 | |||||||||||||||||||||||||
| -6 | 849 850 |
| -6 | |||||||||||||||||||||||||
| -5 | 851 852 |
| -5 | |||||||||||||||||||||||||
| -4 | 853 854 |
| 
|
| -20 | |||||||||||||||||||||||
| -3 | 855 856 |
| 
|
| -15 | |||||||||||||||||||||||
| -2 | 857 858 |
|
|
| -8 | |||||||||||||||||||||||
| -1 | 859 860 |
|
|
|
| -8 | ||||||||||||||||||||||
| 861 862 |
|
|
|
| ||||||||||||||||||||||||
| 863 864 |
|
| ||||||||||||||||||||||||||
| 865 866 |
|
|
| 
|
|
|
| |||||||||||||||||||||
| 867 868 |
| 
|
|
|
| 
|
| |||||||||||||||||||||
| 869 870 |
|
|
|
|
|
| ||||||||||||||||||||||
| 871 872 |
| 
|
|
| ||||||||||||||||||||||||
| 873 874 | ||||||||||||||||||||||||||||
| 875 876 | ||||||||||||||||||||||||||||
| 877 878 |
| |||||||||||||||||||||||||||
| Σy’ ny’ | Σy’ ny’ y’ | Σy’ ny’ (y’)2 | ||||||||||||||||||||||||||
| nx’ | 
| |||||||||||||||||||||||||||
| nx’ x’ | -8 | -12 | -5 | -4 | -24 | -4 | -14 |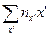 
| ||||||||||||||||||||
| nx’ (x’)2 |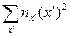 
| |||||||||||||||||||||||||||
| Σnx’y’ y’ | -7 | -16 | -6 | -4 | -20 | -2 | -8 |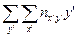 
| ||||||||||||||||||||
| Σnx’y’ y’x’ | 
|
Вычисляем произведения значений колонки 1 на 
и заполняем 3-ю колонку. Суммируя значения этой колонки, найдем, что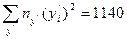 
.
Определяем произведения значений на соответствующие значения 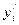, суммируем эти произведения и заполняем строку 4.
Например: 1×(-7)=-7; 2×(-8) = -16; 1×(-6) = -6; 1× (-4) = -4;
1×(-5) + 3(-4) + 1×(-3 ) + 2×(- 1)+ 1×2 =- 5- 12- 3- 2 +2- -20 и т. д.
Суммируя все значения этой строки, определяем 
. Контролем правильности предыдущих вычислений служит равенство сумм значений 4-й строки и2-й колонки, т. е.
.
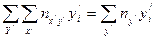Значения 4-й строки умножаем на и заполняем строку 5. Сумма значений этой строки равна
.
Вычисленные значения сумм подставляем в формулу (d) и определяем эмпирическое значение коэффициента корреляции
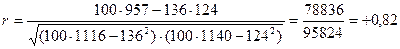
После того, как определен коэффициент корреляции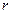 
, необходимо оценить существенно ли отличие полученного значения 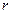от 0.
Для решения этой задачи можно воспользоваться способом Фишера [*].
Случайная величина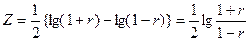
, подчинена нормальному закону со средним квадратическим отклонением
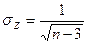. Значения Z для различных r приведены в приложении 4.
В рассматриваемом примере:
. По приложению 4 находим, что для r = 0,82; Z = 1,1568.
Определяем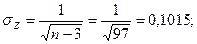 
По найденному значению t по приложению 5 находим Ф(t). Вероятность того, что отклонение
от 0 случайно равно 
. В примере для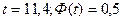 
. Поэтому 
За уровень значимости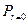 
обычно принимают 0,05 или 0,01, Если 
, то значение 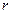можно считать полученным случайно, а исследуемые случайные величины некоррелятивными.
Так как коэффициент корреляции 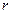является случайной величиной, то иногда требуется по эмпирическому значению 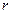оценить теоретическое значение коэффициента 
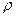, т. е, найти такой интервал, в котором с заданной надежностью находится значение .
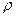Зададимся надежностью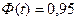 
, т.е.
. Это равенство выполняется при 
. Случайная величина 
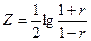имеет среднее квадратическое отклонение .
____________________________________
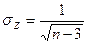* Смирнов Н.В., Дунин-Барковский И.В. Краткий курс математической статистики для технических приложений, М., Физматгиз, 1959.
Поэтому 
.
Определив доверительный интервал для Z, по приложению 4 находим значения для.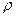
Рассмотрим предыдущий пример. Величина . По приложению 4 находим Z = 1,1568.
Вычисляем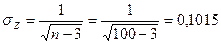 
.
Задаемся надежностью Ф(t)= 0,95. При этом t = 1,96.
Определяем доверительный интервал для 
, т. е. для Z, соответствующему теоретическому значению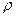
или 
.
Пользуясь приложением 4 для найденных Z=1,0579 и 1,3557, находим значения .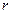
Для Z = 1,0579, r = 0,79 и для Z= 1,3557, 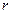= 0,89.
Поэтому 0,79 <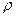< 0,89, т. e. теоретическое значение коэффициента корреляции с вероятностью 0,95 лежит в этом интервале.
ПРИЛОЖЕНИЯ
Приложение 1
Плотность вероятности нормального распределения 
| t | ||||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 | 0,3989 0,2420 0,0540 0,0044 |
Приложение 2
Таблица вероятностей P для критерия К. Пирсона c2
 к
| ||||||||||||||
| 0,6065 | 0,8013 | 0,9098 | 0,9626 | 0,9856 | 0,9948 | 0,9982 | 0,9994 | 0,9998 | 0,9999 | 0,9994 | 0,9998 | 0,9999 | 0,9996 | |
 к
| ||||||||||||||
| 0,9998 | 0,9999 | 0,9998 | 0,9999 | 0,9997 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 |
Приложение 3