Сложение гармонических колебаний одинакового направления

Решение ряда вопросов, в частности, сложение нескольких колебаний одинакового направления, значительно облегчается, если изображать колебания графически, в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой.

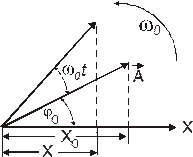Рис. 8.1

Из точки O, взятой на оси x построим вектор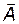, образующий с осью угол j0 (рис. 8.1).

Проекция этого вектора на осьx равна

 

x=Acosj₀.

 

Предположим теперь, что вектор 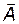равномерно вращается с угловой скоростью w0. Тогда за время t он опишет угол, равный w0t, и новая проекция этого вектора на ось х станет равной:

 

x=Acos (w0t+j0).

 

Следовательно, проекция конца вектора 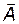на ось x будет совершать гармонические колебания с амплитудой, равной длине вектора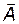, с частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью x в начальный момент времени. Из сказанного следует, что гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью x угол, равный начальной фазе колебаний.

Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты:

 

 

x₁=A₁ cos(w₀t+j₁); x₂=A₂ cos(w₀t+j₂).

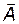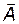Представим оба колебания с помощью векторов ₁ и₂, образующих с осью х углы j₁ и j₂ соответственно (рис. 8.2). Построим по правилу сложения векторов результирующий вектор 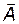p. Легко видеть, что проекция этого вектора на осьх равна сумме:

 

x=x1 + x2.

 

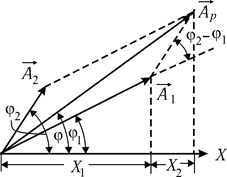Рис. 8.2

Вектор 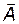p вращается с той же угловой скоростью, как и векторы 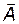₁ и 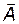₂, так что результирующее движение будет гармоническим колебанием с частотой w₀, амплитудой А_p и начальной фазой j:

 

X=Ap cos(w₀t+j).

 

Найдём теперь из векторной диаграммы результирующую амплитуду. По теореме косинусовимеем:

 

.

(8.1)

 

Упражнение. Рассмотрите, чему будет равна результирующая амплитуда колебаний, если: a) j₂ - j₁ = 0; б) j₂ - j₁ = p.