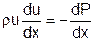Уравнение движения
Уравнением движения выражает закон сохранения импульса, поэтому его называют также «уравнение импульсов» или «уравнение количества движения».
Снова рассмотрим элемент канала с бесконечно малой длиной dx (рис. 1).
В начальный момент времени t выделим массу газа, находящуюся между сечениями канала «x» и «x+dx». Эта масса представляет собой физическое тело, изменение импульса которого будет интересовать нас в дальнейшем.
На левой границе выделенного объема параметры равны {u, r, P, T}. На правой границу – {u+du, r+dr, P+dP, T+dT}, причем du=(du/dx)dx и аналогично для всех других параметров.
Левая граница выделенного тела за промежуток времени между «t» и «t+dt» перемещается на расстояние udt. Правая – на (u+du)dt. Рассмотрим часть объема канала, находящуюся между левой границей «нового» положения тела и правой границей «старого». Количество движения – это произведение массы тела на его скорость. Поскольку течение стационарное, количество движения газа, находящегося в этом объеме в момент времени «t», равна количеству движения газа, находящегося там же в момент «t+dt». Поэтому импульс выделенного физического тела в момент «t+dt» можно выразить следующим образом:

Второй (отрицательный) член в правой части – это импульс газа, заключенного между левой границей «старого» положения и левой границей «нового» положения выделенного физического тела. udt – это продольный размер, F – площадь сечения, поэтому uFdt – это объем, ruFdt – масса, а ru2Fdt – импульс. Третий член (положительный) – это, аналогично, импульс газа, находящегося между правыми границами.
Закон, по которому изменяется импульс тела (второй закон Ньютона):
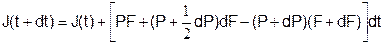
Предполагается, что на выделенное физическое тело действуют только силы давления на торцевых поверхностях и на боковой поверхности. Проекция силы давления на продольную ось на левой границе – «PF», на правой – «-(P+dP)(F+dF)», на боковой поверхности – «(P+(1/2)dP)dF».
Объединяем два последних выражения, затем раскрываем скобки и пренебрегаем членами с порядком малости выше первого. Получается:
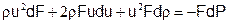
С использованием закона сохранения массы: левая часть упрощается до rFudu. Тогда:
левая часть упрощается до rFudu. Тогда:

Это и есть окончательная форма уравнения импульсов для стационарного одномерного потока, которое является следствием закона сохранения количества движения.
Необходимо понимать определенную терминологическую проблему: хотя импульс тела, вообще говоря, меняется, используется название «закон сохранения импульса», по аналогии с «законом сохранения массы», которая, в отличие от импульса, действительно остается постоянной.
Помня о том, что дифференциалы всех величин выражаются через их производные по единственной независимой переменной «x», уравнение импульсов для стационарного одномерного потока можно записать следующим образом: