УРАВНЕНИЕ ШРЕДИНГЕРА
Рассмотрим простой пример движения частицы. Пусть ее состояние таково, что координата частицы имеет определенное значение x. Это значит, что соответствующий вектор |cxñ есть собственный для оператора координаты  :
:
 |cxñ = x|cxñ.
|cxñ = x|cxñ.
Разложим по всем таким состояниям произвольный вектор |yñ:
|yñ = òdx|cxñácx|yñ,
где учтено, что из физических соображений спектр координаты - чисто непрерывный. Таким образом, вектор |yñ задается континуальным множеством чисел
ácx|yñ º y(x),
т.е. фактически некоторой функцией y(x) от x. Она называется волновой функцией частицы. Из нормированности вектора |yñ имеем:
1 = áy|yñ = òdxRdxáy|c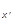 ñác
ñác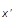 |cxñácx|yñ =
|cxñácx|yñ =
= òdxRdxáy|c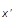 ñ d(x-xR)ácx|yñ = òdxy*(x)y(x)dx = òdx|y(x)|2,
ñ d(x-xR)ácx|yñ = òdxy*(x)y(x)dx = òdx|y(x)|2,
т.е. волновая функция нормируется условием
ò|y(x)|2 dx = 1.
Волновая функция y(x) -это координатная реализация вектора |yñ состояния y из абстрактного гильбертова пространства квадратично интегрируемой функцией, т.е. вектором из функционального пространства L2. Если векторы |y1ñ и |y2ñ нормируемы, то их скалярное произведение теперь запишется как функциональное скалярное произведение:
áy1|y2ñ = òdxy*1 (x)y2 (x)
(доказательство такое же, как при получении условия нормировки).
Возьмем произвольный вектор |yñ, подействуем на него оператором  и введем обозначение
и введем обозначение
 |yñ º |
|yñ º | ñ.
ñ.
Для волновой функции состояния  имеем:
имеем:
 (x) = ácx |
(x) = ácx | ñ = ácx|
ñ = ácx| |yñ º (cx,
|yñ º (cx, y) = (
y) = ( cx,y) =
cx,y) =
= x (cx,y) = xyx.
Таким образом,
 y(x) = xy(x) Û
y(x) = xy(x) Û  = x,
= x,
т.е. в координатной реализации оператор  есть просто оператор умножения на независимую переменную x. Для среднего значения координаты в состоянии y имеем:
есть просто оператор умножения на независимую переменную x. Для среднего значения координаты в состоянии y имеем:
áxñy = áy | |yñ º áy1|y2ñ = òy*1 (x)y2 (x)dx =
|yñ º áy1|y2ñ = òy*1 (x)y2 (x)dx =
= òy* (x){xy(x)}dx,
т.е.
áxñy = òdx×x|y(x)|2.
Это выявляет физический смысл волновой функции - квадрат ее модуля |y(x)|2 задает плотность вероятности обнаружить частицу в точке с координатой x. Результат ясен и из общей теории - из определения y(x) как ácx|yñ и из вероятностной интерпретации ácx|yñ (см. РЕЗЮМЕ). Можно сказать также, что y(x) = ácx|yñ есть амплитуда вероятности перехода частицы из состояния y в состояние cx (см. постулат II).
Вообще говоря, волновая функция зависит не только от координаты, но и от времени. В фиксированный момент времени t0 функция y(x,t0) однозначно определяет состояние y. Очевидно из принципа причинности, что она должна определять и дальнейшую эволюцию системы, т.е. состояние y в произвольный момент времени t, т.е. волновую функцию y(x,t). Поэтому волновая функция должна подчиняться некоторому дифференциальному уравнению первого порядка по времени, для однозначного отыскания решения которого как раз и достаточно задать y(x,t0), (но не ее производные). Поэтому можно записать
 .
.
Здесь множитель i выделен для удобства (чтобы было 
 =
=  - см. ниже), а
- см. ниже), а  - некоторый дифференциальный оператор, не включающий производных по времени. Он должен быть линейным, чтобы соблюсти принцип суперпозиции.
- некоторый дифференциальный оператор, не включающий производных по времени. Он должен быть линейным, чтобы соблюсти принцип суперпозиции.
Докажем эрмитовость оператора  . Имеем очевидное равенство
. Имеем очевидное равенство
 ,
,
так как дифференцируется полная вероятность, т.е. 1. Вносим производную под знак интеграла и дифференцируем:
 .
.
Подставляем производные 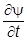 и
и  из уравнения и сопряженного ему:
из уравнения и сопряженного ему:
 ,
, 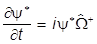 .
.
Получаем
0 = ò dx (y* +y - y*
+y - y* y),
y),
т.е.
 y*
y* ydx = ò
ydx = ò +ydx Û (y,
+ydx Û (y, y) = (y,
y) = (y, y).
y).
В силу произвольности y это и означает эрмитовость  :
:
 =
=  +.
+.
Рассмотрим систему, на которую не действуют нестационарные внешние силы. Это значит, что оператор  не зависит от времени, и решение уравнения можно искать методом разделения переменных. Ищем частное решение в виде
не зависит от времени, и решение уравнения можно искать методом разделения переменных. Ищем частное решение в виде
y(x,t) = Q(t)y(x)
и подставляем в уравнение
 ,
,
где w - константа разделения переменных, не зависящая от x и t. Для Q(t) сразу получаем решение
Q (t) = const.e-iwt.
Значения же w находятся как собственные значения оператора  :
:
 y(x) = wy(x).
y(x) = wy(x).
Их может быть много, а значит, будет много и частных решений с разными w. Считая их спектр дискретным, запишем общее решение как
y(x,t) = 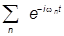 yn (x)
yn (x)
(коэффициенты линейной комбинации включаем в yn (x)).
Разложим функции yn (x) в интеграл Фурье и подставим в y(x,t):
y(x,t) = 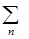 òdk
òdk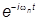 +ikx
+ikx (k).
(k).
Вводя обозначения
E º iw, p º ik,
получим:
y(x,t) =  òdp
òdp
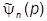 ,
,
где

 .
.
Смысл E-энергия, p - импульс (см. волны де Бройля в лекции 1).
Теперь мы хотим извлечь отсюда явный вид операторов энергии и импульса. Для этого сделаем отступление. Пусть  - произвольный оператор, и |jnñ - его собственные функции. Разложим по ним произвольный вектор |yñ:
- произвольный оператор, и |jnñ - его собственные функции. Разложим по ним произвольный вектор |yñ:
|yñ =  cn|jnñ
cn|jnñ
и подействуем на него оператором :
:
 |yñ =
|yñ =  cnAn|jnñ .
cnAn|jnñ .
Характерный признак действия оператора на разложение: он «вышибает» из каждого слагаемого соответствующее свое собственное значение. Берем теперь найденное разложение для y(x,t) и действуем на него оператором
и действуем на него оператором 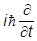 :
:
 y(x,t) =
y(x,t) =  òdpEn
òdpEn 
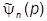
Так как «вышиблись» значения энергии En, то оператор энергии есть
 =
=  .
.
Аналогично,
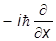 y(x,t) =
y(x,t) =  òdp×p
òdp×p
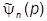 ,
,
а потому оператором импульса является
 =
= 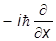 .
.
Возьмем теперь наше исходное уравнение и умножим его обе части на i:
 = i
= i y(x,t).
y(x,t).
Слева стоит оператор энергии, а значит справа - оператор Гамильтона
i =
=  .
.
В итоге приходим к основному динамическому уравнению квантовой механики - к уравнению Шредингера
 =
=  y(x,t).
y(x,t).
Мы рассмотрели одномерный случай. В трехмерном случае y = y(r,t), где r=(x, y, z). Общее решение уравнения Шредингера запишется как
y(r,t) =  òdp
òdp
 .
.
Операторы
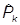 =
= 
есть операторы k-х компонентов импульса. Сам же оператор вектора импульса будет таким:
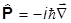 .
.
Чтобы записать в явном виде уравнение Шредингера, надо знать явный вид оператора Гамильтона  . Он строится по принципу соответствия. Один из его аспектов гласит:
. Он строится по принципу соответствия. Один из его аспектов гласит: