НОРМИРОВКА В НЕПРЕРЫВНОМ СПЕКТРЕ
Итак, классическому финитному движению отвечает в квантовой механике состояния с нормируемыми волновыми функциями, которые можно нормировать на 1, а энергетический спектр является дискретным. Классическому инфинитному движению отвечают состояния с обобщенными волновыми функциями, которые нельзя нормировать, а энергетический спектр является непрерывным.
Возникает проблема нормировки волновых функций непрерывного спектра. Раньше мы их нормировали, и обычно так и делают, на дельта- функцию. Однако этот прием достаточно формален. Реально же на самом деле спектр всегда является дискретным, так как размеры области локализации частицы ограничены хотя бы стенками лаборатории. Правда, часто случается так, что L>>l, где L - размеры лаборатории, а l - размеры физической системы. Влияние стенок оказывается пренебрежимо малым, и энергетические уровни расположены столь тесно, что спектр невозможно отличить от непрерывного. Ведь в предыдущей задаче величина L2 входила в знаменатель En, и чем она больше, тем гуще спектр.
Но реальная физическая ситуация делает оправданной так называемую «нормировку в ящике», когда частица считается находящейся в ограниченной области, хотя и больших размеров по сравнению с ее собственными размерами. Итак, все пространство разбивается на ящики и частица сажается в один из них. Так как ящик велик, влияние стенок мало и на них можно поставить любые дополнительные условия - условия Бора - Кармана - условия периодичности: требуется, чтобы волновая частица повторялась в каждом ящике. В одномерном случае это записывается как
y(x+L) = y(x).
От такой волновой функции и требуется, чтобы
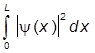 =1
=1
Рассмотрим в качестве примера вновь свободную частицу с уравнением Шредингера
-i2/2m ×yRR = Ey
с волновыми функциями
y(x) = Aei/i px ; E = p2/2m,  ,
,
(импульс строго определен). Накладываем условие периодичности:
Aei/i p(x+L) = Aei/i px,
откуда
ei/i pL = 1 Þ pL/I = 2pn, nÎZ.
Получаем дискретный ряд значений для импульса и для энергии:
pn = 2pi/L×n, En = 2p2i2n2/mL2 .
При больших L спектр оказывается практически непрерывным, а нормировочная константа
A = 
Это получается так же, как в задаче о частице в яме, где нормировочная константа как раз и была равной
A = 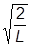
(двойки теперь нет потому, что немножко другие граничные условия - не нулевые, а периодические).