СМЕШАННЫЕ СОСТОЯНИЯ И МАТРИЦА ПЛОТНОСТИ

 

До сих пор мы описывали состояния микросистемы векторами гильбертова пространства |yñ и волновыми функциями y(q) в каком-то заданном q-представлении. Это есть максимально полное квантовомеханическое описание состояний, и они называются чистыми состояниями. Но бывает и так, что для некоторых состояний мы не располагаем всей информацией, необходимой для сопоставления им векторов |yñ или волновых функций y(q). Такие состояния называются смешанными, и их способ описания - иной.

Начнем с достаточно простого случая системы двух частиц 1 и 2. Для системы из одной частицы 1 пусть волновая функция есть y⁽¹⁾ (q₁), а базисные функции обозначим как j_n⁽¹⁾(q₁), так что

 

y⁽¹⁾ (q₁) = j_n⁽¹⁾(q₁).

Для системы одной частицы 2 аналогично пусть волновая функция y⁽²⁾ (q₂), а базис образует j_m⁽²⁾(q₂):

 

y⁽²⁾ (q₂) = j_m⁽²⁾(q₂).

Если в двухчастичной системе 1-2 отдельные частицы не взаимодействуют, то ее волновая функция есть произведение одночастичных:

 

y (q₁,q₂) = y⁽¹⁾ (q₁)y⁽²⁾ (q₂) = j_n⁽¹⁾(q₁)j_m⁽²⁾(q₂).

 

Но в общей ситуации, когда частицы взаимодействуют, полную волновую функцию нельзя представить в виде произведения одночастичных. Базис здесь образуют всевозможные произведения j_n⁽¹⁾(q₁)j_m⁽²⁾(q₂), и можно записать разложение

 

y(q₁,q₂) = j_n⁽¹⁾(q₁)j_m⁽²⁾(q₂).

 

Однако, коэффициенты C_nm уже нельзя представить в прежней форме

 

C_nm ¹ C_n⁽¹⁾C_m⁽²⁾.

 

Введем обозначение

 

C_nmj_m⁽²⁾(q₂) º f(q₂)

 

и представим общее разложение в форме

 

y(q₁,q₂) = 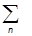f_n(q₂)j_n⁽¹⁾(q₁).

 

Пусть теперь нас интересуют характеристики частицы 1 в общей двухчастичной системе 1-2. Например, пусть нас интересует среднее значение какой-то наблюдаемой этой частицы - скажем, ее импульса 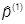. Тогда в отсутствие взаимодействия мы получим:

 

=

 

,

 

r_nn’ º C_n^(1)*C_n’⁽¹⁾.

 

Видим, что в случае невзаимодействующих частиц среднее значение наблюдаемой частицы 1 определяется только ее волновой функцией, а наличие частицы 2 вообще несущественно. Это и естественно, поскольку частицы не влияют друг на друга.

Но пусть теперь взаимодействие присутствует. Тогда

 

 

 

=

 

.

 

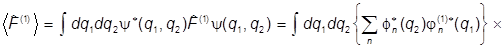
Здесь введена матрица плотности

 

r_{nn’ º}dq₂f^*_n(q₂)j_n’⁽¹⁾(q₁).

 

Формально среднее от вычисляется с ее помощью так же, как в предыдущем случае. Но если там (в отсутствие взаимодействия) матрица плотности r⁽¹⁾_nn’ определялась исключительно поведением частицы 1, то теперь (в общей ситуации) в нее уже входит и поведение частицы 2. Таким образом, при наличии взаимодействия состояние частицы 1 (с точки зрения возможности вычисления средних значений) не может быть описано какой-то волновой функцией вида y(q₁). Это состояние описывается матрицей плотности, которая включает характеристики не только частицы 1, но и всей системы в целом. Такое состояние частицы 1 (но не всей системы!) и является смешанным. В нашем примере оно возникло потому, что, строго говоря, частица 1 не образует систему - она есть подсистема более широкой системы 1-2. И естественно, что ее описание самой по себе будет неполным.

Теперь мы хотим ввести понятие смешанного состояния и его характеризации в самой общей ситуации. Для этого начнем с чистого состояния y, которое описывается вектором |yñ и несколько переформулируем известные нам положения. Интересовать нас будут прежде всего средние значения наблюдаемых в заданных состояниях. В обычном формализме

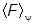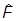= áy||yñ.

 

Введем ортонормированный базис |nñ и перепишем эту формулу, два раза используя разложение единицы:

 

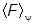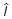
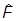
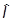= áy||yñ = .

 

Величина

 

есть оператор - проектор на вектор |yñ. Назовем его статистическим оператором данного чистого состояния y. Величины

 

 

образуют матрицу статистического оператора. Назовем ее матрицей плотности данного чистого состояния y. Величины

 

án|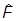|n^’ñ ºF_nn^’

 

образуют матрицу оператора 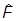в заданном базисе. Таким образом,

 

= ,

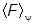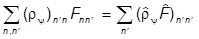или

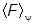= Sp.

 

Итак, среднее значение наблюдаемой F в состоянии y можно вычислять или задавая вектор состояния |yñ, или задавая статистический оператор 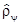(матрицу плотности). Покажем, что это же справедливо и для вероятностей. Пусть нас интересует вероятность Wy(f) получить при измерении наблюдаемой F в состоянии y значение f. Считая для простоты записи спектр дискретным и простым, получим:

 

= ,

 

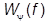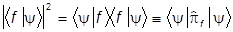где введен оператор проектирования

 

 

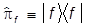
на собственный вектор оператора 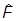, отвечающий интересующему нас собственному значению f . Вычисление вероятности сводится к вычислению среднего значения этого оператора в состоянии y, а потому, согласно предыдущему,

 

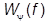= Sp.