Элементарная функция

Функция называется элементарной, если она получена из основных элементарных функций с помощью конечного числа алгебраических действий и операций образования сложной функции.

Например, функция

является элементарной, так как она получена из основных элементарных функций: степенной 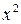и тригонометрической с помощью операции сложения.

Функция

является элементарной, так как она получена из основных элементарных 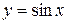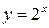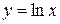функций: , , , , , с помощью конечного числа алгебраических операций сложения, вычитания, умножения, деления и операций образования сложной функции.

Примеры неэлементарных функций: функция Дирихле (рис.7); функция y=[x] (читается «y равно антье x») – целая часть от значений аргумента x (рис.8).

Функция Дирихле:

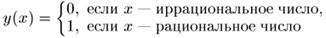
определена на всей числовой прямой; множество ее значений состоит из двух точек: 0 и 1. График ее изобразить невозможно. На рис.7 приведено лишь схематическое изображение функции Дирихле.

Функция y=[x] задана для вещественных значений x (x є R), а множество ее значений состоит из целых чисел (y є Z) (рис.7).

 

Рис.7 Рис.8

Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).

Функция называется алгебраической, если над ее аргументом проводится конечное число алгебраических действий (сложение, вычитание, умножение, деление). Алгебраические функции тесно связаны со степенными. К ним относятся:

- Многочлен (полином) – целая рациональная функция P_n(x):

.

Здесь – постоянные числа (коэффициенты); nÎN – степень многочлена. Функция определена на всей числовой оси.

К целым рациональным относятся распространенные линейная (степень n=1) и квадратичная (n=2) функции.

- Дробно-рациональная функция – отношение двух многочленов P_n(x)/ Q_m(x):

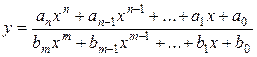
- Иррациональная функция – если в составе операций над аргументом имеется извлечение корня.

Неалгебраические (трансцендентные) функции получают из показательной, логарифмической, тригонометрических, обратных тригонометрических функций.