Обратная функция

Пусть функция у=f(x) отображает область определения D на область значений E взаимно однозначно, т.е. каждому значению х из области D соответствует единственное значение у из области E, и обратно, каждому у из E соответствует единственное значение х из D. Тогда можно задать функцию x=j(y), обратную к y=f(x) следующим образом:

Если каждому , то каждому .

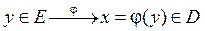Функции f и j называются взаимно обратными.

Функцию, обратную данной функции f, обозначают f^-1 или x=f^-1(y), . Для обратной функции f^-1 множество D – область значений, множество Е – область определения.

Для задания обратной функции f^-1 надо решить уравнение y=f(x) относительно х (если это возможно), выразив х через у: x=f^-1(y).

Пример. Для функци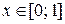й , и , найти обратные к ним функции, если последние существуют.

Решение. Для функции , 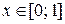функция , 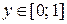является обратной (рис.9).

У функции , не существует обратной, так как разным х₁ и х₂ может соответствовать один и тот же y. Например, числам 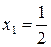и соответствует одно и то же число 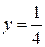(рис.10).

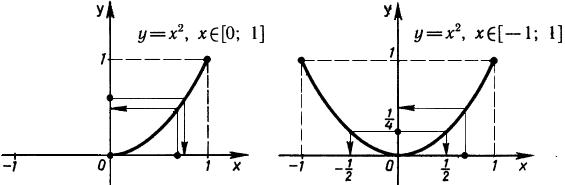
Рис.9 Рис.9

Однако традиционно независимую переменную обозначают через x, а функцию через y, поэтому функция, обратная к функции y=f(x), примет вид

y=φ(x)=f^-1(x).

Например, для функции , 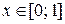обратной будет функция , . Для функции y=a^x обратной будет функция y=log_ax.

Существует теорема, что для любой строго монотонной функции у=f(x) существует обратная функция.

Графики взаимно обратных функций у=f(x) и y=j(x) симметричны относительно биссектрисы I и III координатных углов, то есть прямой y=x (рис.11).

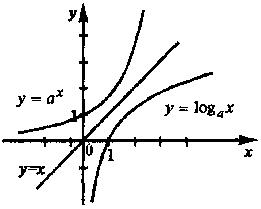
Рис. 11