Числовые характеристики случайных величин, отражающих особенности распределения.

Определение 1.Модой 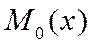случайной величины Х называется ее наиболее вероятное значение (для которого вероятность 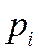или плотность вероятности 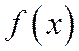достигает максимума).

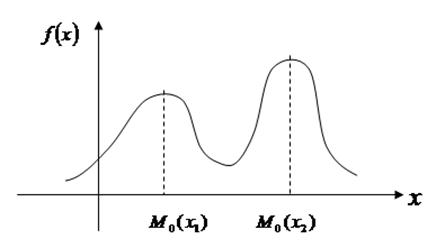
Если вероятность или плотность вероятности достигает 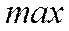не в одной, а в нескольких точках, то распределение называют полимодальным.

Определение 2. Медианой 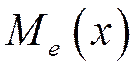непрерывной случайной величины Х называется такое ее значение, которое определяется равенством:

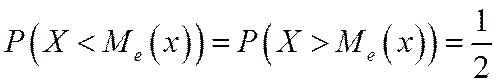
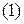
То есть вероятность того, что случайная величина Х примет значение меньше медианы 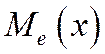или больше ее, одна и та же и .

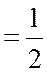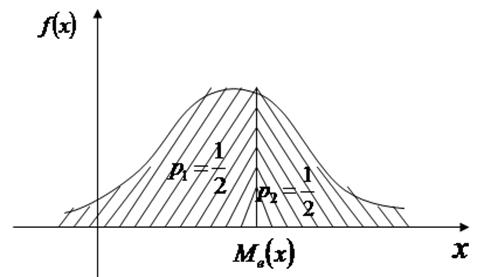
Геометрически: вертикальная прямая 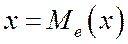, проходящая через точку с абсциссой = 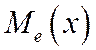, делит площадь фигуры под кривой распределения на две равные части.

Пример: Найти моду, медиану и 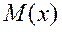случайной величины Х с плотностью вероятности 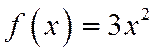при

Построим кривую распределения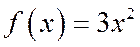

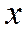
			½
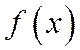
			3/4

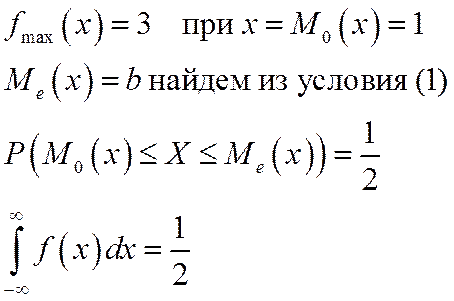
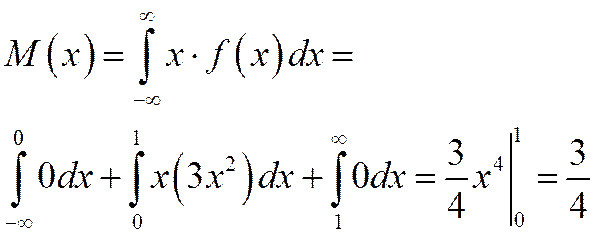
Определение 3.Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-й степени этой величины.

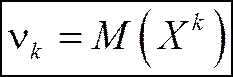
Для дискретной случайной величины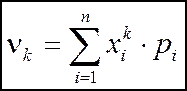

Для непрерывной случайной величины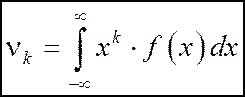

Определение 4. Центральным моментом

k-го порядка случайной величины Х называется математическое ожидание k-й степени отклонения случайной величины Х от ее математического ожидания.

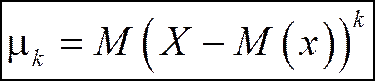
Для дискретной случайной величины:

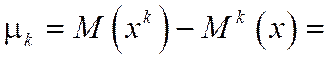
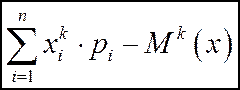
Для непрерывной случайной величины:

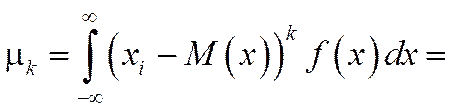
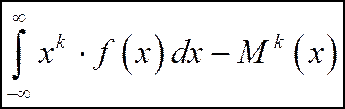
Нетрудно заметить, что при 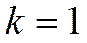первый начальный момент случайной величины Х есть ее математическое ожидание, т.е. , при - второй центральный момент – дисперсия, т.е. .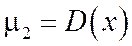

Центральные моменты могут быть выражены через начальные моменты 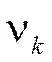по формулам:

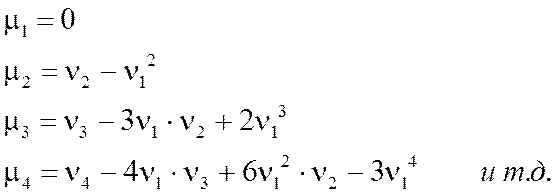
Итак, первый начальный момент характеризует среднее значение или положение распределения случайной величины Х или ее .

Второй центральный момент - степень рассеивания распределения Х относительно 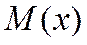- или .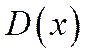

Третий центральный момент 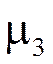служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Поэтому, чтобы получить безразмерную величину, ее делят на .

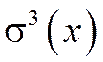Определение 5.Коэффициентом асимметрии А называется величина, равная отношению третьего центрального момента к кубу среднего квадратического отклонения.

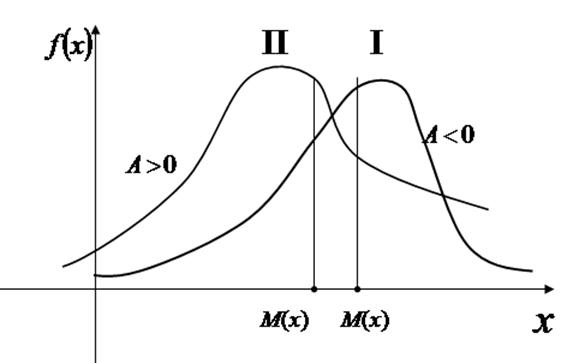
I. Если коэффициент асимметрии отрицательный, то это говорит о большом влиянии на величину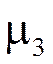отрицательных отклонений. В этом случае кривая распределения более полога слева от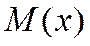(левосторонняя асимметрия).

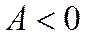II. Если коэффициент, а значит, преобладает влияние положительных отклонений, то кривая распределения более полога справа от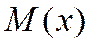(правосторонняя асимметрия).

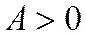Четвертый центральный момент 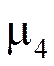служит для характеристики крутости (островершинности или плосковершинности) распределения.

Определение 1. Эксцессом случайной величины называется число:

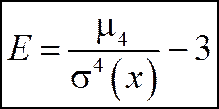
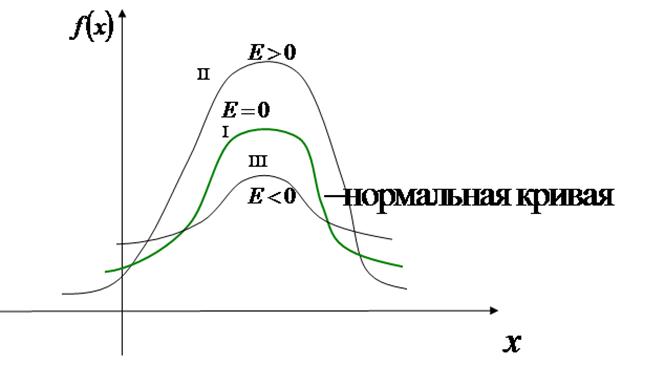
I. Для наиболее распространенного в природе нормального закона распределения (который будет рассматриваться далее) отношение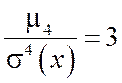. Поэтому эксцесс служит для сравнения данного распределения с нормальным, у которого.

 

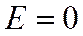II. Если для данного распределения 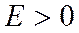, то соответствующая кривая распределения более островершинная по сравнению с кривой нормального распределения.

III. Если , то кривая распределения более плосковершинная.

Пример: Случайная величина задана функцией:

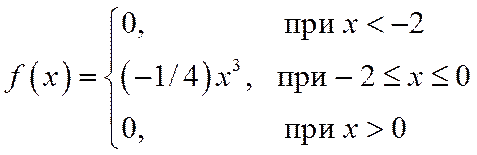
Вычислим начальные моменты до 4-го порядка:

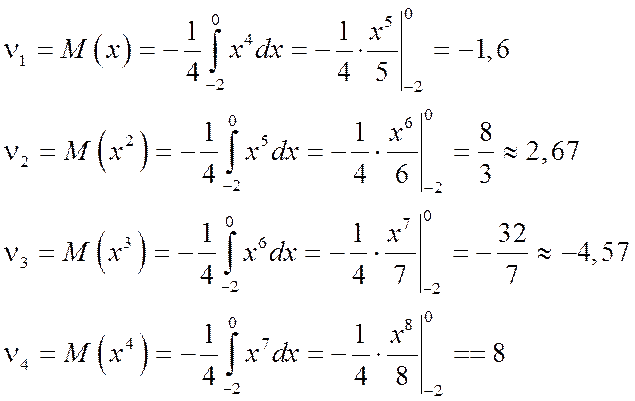
Найдем центральные моменты: