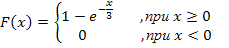Задача 12.2.3.
Случайные величины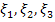 
имеют геометрическое, биноминальное и пуассоновское распределения соответственно. Найти вероятности
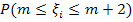, если математические ожидания 
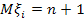, а дисперсия 
.
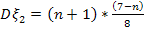Решение:
По условию задачи при значениях параметров m=3, n=3, надо найти
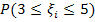, если 
, 
, 
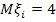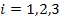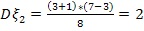
1.Случайная величина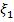 
имеет геометрическое распределения, если её возможные значения 1,2,3,4…. , а вероятности этих значений
.
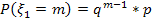Известно, что 
; тогда 
;
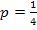так как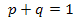 
, тогда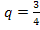 
Вычислим:
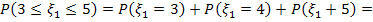
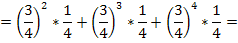
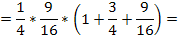
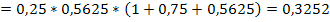
2. Случайная величина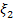 
имеет биноминальное распределение, если она принимает значения 0,1,2,3… с вероятностями:
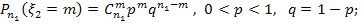
Известно, что:
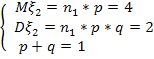тогда, решая эту систему получим:
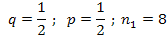
Вычислим:
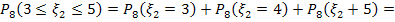
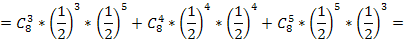
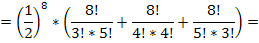
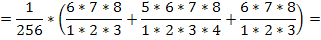
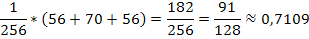
3. Случайная величина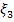 
имеет распределение Пуассона, если ее возможные значения 0,1,2…, а соответствующие вероятности вычисляются по формуле:
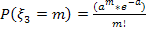, где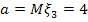 
Тогда:
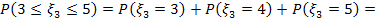
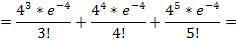
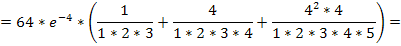
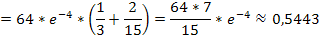
Задача 12.2.4.
Случайные величины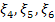 
имеют равномерное, показательное и нормальное распределения соответственно. Найти вероятности
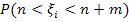, если у этих случайных величин математические
ожидания и среднее квадратические отклонения равны m.
Решение:
Пусть n=2, m=5. Тогда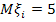 
, 
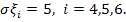Надо найти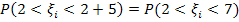 
1. Для равномерно распределенной на отрезке [a,b] случайной величины функция плотности имеет вид.
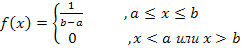
Математическое ожидание вычисляется по формуле:
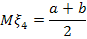
Дисперсия:
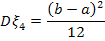
Отсюда, среднее квадратическое отклонение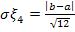 
(
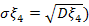
По условию задачи имеем:
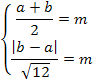
При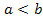 
эта система равносильна системе:
,
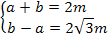решая которую, получаем:
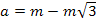
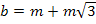
Отсюда:
.
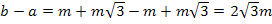Значит, функция плотности имеет вид:
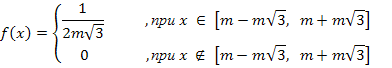
Найдем вероятность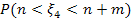 
по формуле попадания значений случайной величины с функцией плотности 
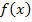в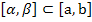 
:
.
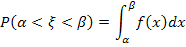
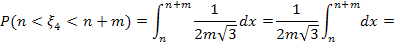
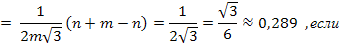
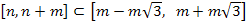Если включение не выполняется, то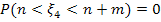 
При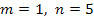 
получаем, что
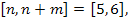
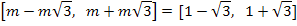
и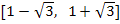 
вне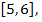 
т.е. на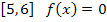 
Тогда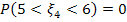 
2. Непрерывная случайная величина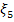 
имеет показательное распределение, если ее плотность вероятности:
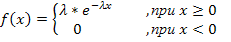
где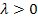 
параметр распределения,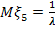 
Функция распределения показательного распределения имеет вид:
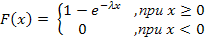
Известно, что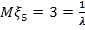 
, отсюда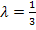 
Тогда:
