Теорема об изменении кинетической энергии.
Рассмотрим движение точки под действием силы 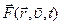 . Динамическое уравнение движения материальной точки запишем в виде:
. Динамическое уравнение движения материальной точки запишем в виде: 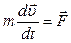 . Умножим это уравнение скалярно на величину
. Умножим это уравнение скалярно на величину 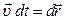 :
:  . Это можно записать так:
. Это можно записать так: 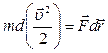 . Поскольку
. Поскольку  , то:
, то: 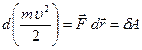 . Выражение, стоящее под знаком дифференциала, называют кинетической энергией точки:
. Выражение, стоящее под знаком дифференциала, называют кинетической энергией точки: 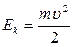 .
.
Соотношение 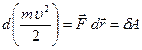 показывает, что бесконечно малое изменение кинетической энергии материальной точки равно элементарной работе сил, действующих на материальную точку. Кинетическая энергия может возрастать или убывать в зависимости от знака элементарной работы.
показывает, что бесконечно малое изменение кинетической энергии материальной точки равно элементарной работе сил, действующих на материальную точку. Кинетическая энергия может возрастать или убывать в зависимости от знака элементарной работы.
Проинтегрируем данное уравнение:
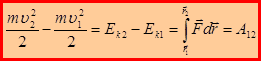
Эта формула выражает математическую запись теоремы об изменении кинетической энергии материальной точки: изменение кинетической энергии материальной точки равно работе силы, действующей на материальную точку.
Если материальная точка движется в потенциальном поле, то работа сил может быть найдена по формуле:  . Введя величину
. Введя величину 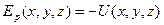 получим:
получим:
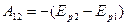
Величина 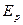 имеет размерность энергии. Ее называют потенциальной энергией материальной точки. Потенциальная энергия материальной точки определяется не однозначно, а с точностью до произвольной постоянной. Это не может отразиться на физических выводах, так как ход физических явлений может зависеть не от значений самой потенциальной энергией, а лишь от ее разности в различных состояний. Эти же разности от выбора произвольной постоянной не зависят. Для примера рассмотрим силу тяжести:
имеет размерность энергии. Ее называют потенциальной энергией материальной точки. Потенциальная энергия материальной точки определяется не однозначно, а с точностью до произвольной постоянной. Это не может отразиться на физических выводах, так как ход физических явлений может зависеть не от значений самой потенциальной энергией, а лишь от ее разности в различных состояний. Эти же разности от выбора произвольной постоянной не зависят. Для примера рассмотрим силу тяжести:

Следовательно 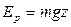 . Неоднозначность в определении потенциальной энергии материальной точки в поле силы тяжести связано с тем что, значение
. Неоднозначность в определении потенциальной энергии материальной точки в поле силы тяжести связано с тем что, значение 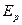 зависит от z, а следовательно и от выбора нулевого уровня, то есть плоскости, где z = 0. Кроме этого ясно, что
зависит от z, а следовательно и от выбора нулевого уровня, то есть плоскости, где z = 0. Кроме этого ясно, что 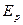 может быть как положительной так и отрицательной и равной нулю.
может быть как положительной так и отрицательной и равной нулю.
ЗАКОН СОХРАНЕНИЯ ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Запишем теорему об изменении кинетической энергии материальной точки:
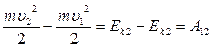
Если сила, действующая на материальную точку, является консервативной:
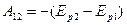
Следовательно:
 или
или 
Сумму кинетической и потенциальной энергий материальной точки называют полной механической энергией материальной точки. Следовательно: полная механическая энергия материальной точки сохраняется, если на материальную точку действует консервативная сила.
В случае действия на материальную точку нескольких сил
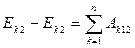
Если все силы консервативны:
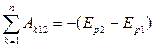

Следовательно, в этом случае также выполняется закон сохранения полной механической энергии материальной точки.
Пусть на материальную точку действуют n сил, но только m из них являются консервативными. При этом получим: 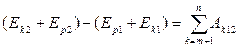 .
.
Изменение полной механической энергии точки равно сумме работ неконсервативных сил, действующих на материальную точку.
В результате вычисления в выражение для работы силы трения явно входит длина пути материальной точки. Эта значит, что сила трения не консервативна. При работе силы трения полная механическая энергия не сохраняется, переходя частично в тепло. Говорят, что в этом случае механическая энергия рассеивается или диссипирует. Поэтому силы трения и другие силы, при работе которых наблюдается переход механической энергии в другие виды энергий, называют диссипативными силами.
материальных точек. Любое материальное тело динамической системы можно мысленно разбить на большое число элементов и заменить эти элементы материальными точками, после этого механическая система рассматривается как совокупность материальных точек. Описать движение механической системы означает описать движение каждой материальной точки этой системы.