Силы и потенциальная энергия

Эту лекцию мы начали с вычисления потенциальной энергии упруго деформированной пружины. Зная характер силы, возникающей при деформации пружины — закон Гука — мы смогли вычислить её энергию.

До этого мы определили потенциальную энергию тела в однородном поле силы тяжести — энергию гравитационного взаимодействия двух частиц. Зная силу электростатического взаимодействия точечных зарядов, можно вычислить и их потенциальную энергию. Теперь зададимся обратной задачей: как определить величину и направление консервативной силы, если известна потенциальная энергия частицы U(x,y,z)?

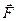Рассмотрим перемещение частицы в поле консервативной силы . При таком перемещении будет совершена работа, равная изменению потенциальной энергии частицы с отрицательным знаком:

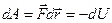. (7.2)

Учитывая, что 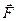= + + 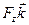и = 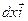+ + 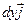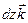, запишем скалярное произведение 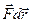в следующем виде:

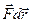= F_xdx + F_ydy + F_zdz = –dU. (7.3)

Теперь представим, что перемещение осуществляется только вдоль направления х. При этом координаты y и z удерживаются неизменными. Тогда dy = dz = 0, а уравнение (7.3) примет вид:

F_x¶x = –¶U.

Откуда x-компонента искомой силы равна:

. (7.4)

Здесь — частная производная потенциальной энергии по координате x в предположении, что y и z постоянны. Формально частная производная определяется так:

.

Для y- и z-компонент консервативной силы можно записать выражения, подобные (7.4):

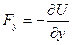, . (7.5)

Объединив формулы (7.4) и (7.5), получим вектор искомой силы:

. (7.6)

В этом уравнении заключено правило, следуя которому можно преобразовать скалярную функцию U в векторную — 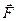. Вот это правило:

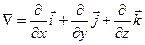. (7.7)

Оно означает, что следует взять частные производные потенциальной энергии по координатам. Придать этим величинам соответствующие направления, домножив их на единичные векторы, и полученные векторы — компоненты силы — векторно сложить.

Это правило — векторный оператор — называется «градиент» или «набла» и обозначается:

.

Таким образом, консервативная сила равна градиенту потенциальной энергии с противоположным знаком:

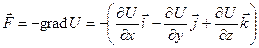. (7.8)

Продолжим рассмотрение движения частицы в потенциальном поле. Потенциальным называется поле консервативных сил.

Если в системе отсутствуют неконсервативные силы, то механическая энергия системы, равная сумме её кинетической и потенциальной энергий, не меняется:

E = E_к + U = сonst.

Так как кинетическая энергия не бывает отрицательной, то U £ E.

Остановимся, ради простоты, на одномерном движении частицы вдоль оси x. Пусть её полная механическая энергия E = U + E_кин равна E₁ = сonst., а зависимость потенциальной энергии представлена графически U = U(x) (рис. 7.3).

График энергии E₁ = сonst. выделяет несколько областей на оси x. В области 1 от х = 0 до х_А частица не может появиться, так как здесь её потенциальная энергия U оказалась бы больше полной энергии E₁. По этой же причине частице недоступна и область 3.

Частица может двигаться в области 2 между точками с координатами х_А и х_В и в области 4: от точки с координатой х_С до х ® ¥.

U

Рис. 7.3

Движение в области 2 — это ограниченное движение в потенциальной яме. Такое движение называется финитным. В положениях х_А и х_В потенциальная энергия частицы равна её механической энергии (U_A = U_B = E₁), то есть в этих положениях кинетическая энергия и скорость частицы равны нулю.

В точке D потенциальная энергия частицы минимальна, а кинетическая энергия = (Е₁ – U_D) достигает максимального значения. В этой точке и скорость частицы максимальна.

Если после точки С (х > х_С) потенциальная энергия U повсюду меньше механической энергии частицы Е₁, то в этой области движение частицы неограниченно. Такое движение называется инфинитным.

 

Лекция 8 «Механика твёрдого тела»

План лекции:

1. Момент силы и момент импульса относительно неподвижного центра и неподвижной оси.

2. Уравнение моментов для материальной точки и системы материальных точек.

3. Закон сохранения момента импульса.

 

Прежде чем приступить к изучению движения твёрдых тел, необходимо познакомиться с рядом новых физических понятий и характеристик движения.