Основное уравнение динамики вращательного движения вокруг неподвижной оси

При вращении твёрдого тела относительно неподвижной оси, все точки тела движутся по плоским круговым траекториям. Выделим частицу m_i тела, вращающегося вокруг оси z (рис. 9.2). Положение частицы зададим радиус-вектором относительно произвольного центра 0, лежащего на оси вращения. R_i — радиус окружности, по которой движется рассматриваемая точка. V_i = wR_i — её линейная скорость.

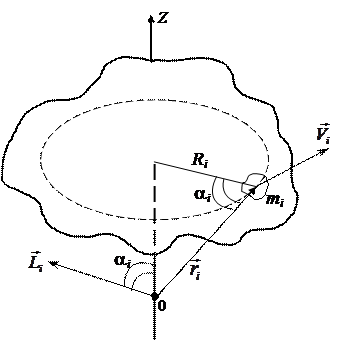
Рис. 9.2

Рассматривая твёрдое тело как неизменную систему материальных точек, для каждой из них можно записать уравнение моментов:

. (9.1)

В левой части этого уравнения — момент внешних сил относительно оси z, действующий на частицу m_i. Справа — производная по времени проекции момента импульса частицы на ту же ось.

Момент импульса частицы относительно центра 0 (по определению) равен:

.

Заметим, что для всех частиц 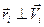, поэтому легко вычислить модуль этого вектора L_i:

L_i = m_ir_iV_i = m_ir_iwR_i.

Так как образует угол a_i с осью z, то проекция этого вектора на ось z равна:

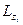= L_iCosa_i = m_ir_iwR_iCosa_i = m_iwR_i(r_iCosa_i) = m_iw. (9.2)

Учитывая этот результат, перепишем уравнение (9.1) ещё раз:

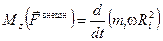. (9.3)

Подобные уравнения могут быть составлены для всех точек твёрдого тела.

Просуммировав все эти уравнения, получим закон вращательного движения твёрдого тела:

или

. (9.4)

Здесь: M_z — суммарный момент всех внешних сил, вращающих твёрдое тело вокруг оси z;

w_z — угловая скорость вращения;

— новая характеристика твёрдого тела — его момент инерции относительно оси вращения;

L_z = I_zw_z — момент импульса тела относительно оси z.

Если момент инерции твёрдого тела I_z не меняется, уравнению (9.4) можно придать такой вид:

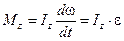. (9.5)

Здесь ε =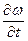— угловое ускорение вращающегося тела.

Уравнение (9.5) называется основным уравнением динамики для твёрдого тела, вращающегося вокруг неподвижной оси.

M_z = I_z×ε (9.6)

Трудно не заметить сходство этого уравнения со вторым законом Ньютона для движения точки:

F_z = ma_z

Сравнивая эти два выражения, отметим, что в уравнении для вращательного движения в качества «силы» выступает момент силы, вместо линейного ускорения — угловое, вместо массы используется момент инерции I_z.

Сходство этих уравнений можно продолжить, записав их иначе (9.2)

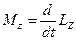
Здесь: L_z = I_z w_x — момент импульса тела относительно оси z,

P_z = mV_z — проекция вектора импульса частицы на ось z.

Во вращательном движении аналогом импульса Р является момент импульса L.

Рассмотренные аналогии позволяют назвать уравнение (9.6) уравнением второго закона динамики (Ньютона) для вращательного движения:

момент внешних сил, вращающих тело вокруг данной оси, равен моменту инерции тела относительно этой оси, умноженному на угловое ускорение тела.

Вернемся ещё раз к уравнению (9.4):

.

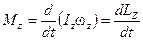Оно в равной степени справедливо как для твердого тела, так и для системы тел. Если момент внешних сил относительно оси z равен нулю, то момент импульса системы относительно этой же оси будет оставаться постоянным.

M_z = 0, Þ 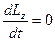Þ L_z = I_zw_z = сonst.

Это закон сохранения момента импульса — аналог закона сохранения импульса замкнутой системы. Но есть между этими законами одно существенное различие. Постоянство импульса частицы (если её масса не меняется) означает неизменность её линейной скорости:

p = mV = сonst. Þ V = сonst.

Если же не меняется момент импульса тела (L_z), то это не означает постоянства угловой скорости:

L_z = I_zw = сonst.

Изменение момента инерции вращающегося тела приведёт к изменению его угловой скорости даже в случае отсутствия внешних вращающих моментов. При этом сохранится неизменным произведение I_z × w = сonst., то есть угловая скорость окажется обратно пропорциональной моменту инерции тела (системы):

.

Известно много примеров, иллюстрирующих эту особенность закона сохранения момента импульса: вращение фигуристов и балерин, опыты на скамье Жуковского, сальто-мортале гимнастов и т.п.