Периодические процессы. Гармонические колебания
Периодическими называются процессы, в точности повторяющиеся через равные промежутки времени: смена дня и ночи, движение поршня в цилиндре двигателя, колебание маятника часов, переменный ток и т.д. (рис. 12.1). Минимальное время, спустя которое процесс повторяется вновь — Т, называется периодом. Математически периодичность функции f(t) записывается так f(t) = f(t + T).

Рис. 12.1
Особое место среди периодических процессов занимают гармонические колебания, когда изменение колеблющейся величины происходит по закону синуса или косинуса (рис. 12.2):
x(t) = a Cos(wt + a). (12.1)

Рис. 12.2
Эту гармоническую функцию удобно графически представить следующим образом. Отложим из точки 0 на оси x вектор  (рис. 12.3). Пусть этот вектор первоначально образует с осью x угол a. Теперь приведем этот вектор во вращение с угловой скоростью w вокруг оси, проходящей через точку 0 перпендикулярно плоскости рисунка. Спустя t секунд угол между вектором и осью x вырастет до значения Ф(t) = (wt + a). Проекция вектора a на ось x окажется при этом функцией времени x(t) = aCos(wt+a) и будет совершать гармонические колебания с частотой w.
(рис. 12.3). Пусть этот вектор первоначально образует с осью x угол a. Теперь приведем этот вектор во вращение с угловой скоростью w вокруг оси, проходящей через точку 0 перпендикулярно плоскости рисунка. Спустя t секунд угол между вектором и осью x вырастет до значения Ф(t) = (wt + a). Проекция вектора a на ось x окажется при этом функцией времени x(t) = aCos(wt+a) и будет совершать гармонические колебания с частотой w.
В этом уравнении: а — амплитуда; w [рад/с] — циклическая частота гармонического колебания; (wt + a) = Ф(t) — фаза колебания. Фаза меняется во времени.
a — значение фазы в момент запуска часов (t = 0), то есть — начальная фаза.
 Процесс повторится вновь спустя Т секунд. За это время фаза должна увеличиться на 2p радиан.
Процесс повторится вновь спустя Т секунд. За это время фаза должна увеличиться на 2p радиан.
[w(t + T) + a] = (wt + a) + 2p;
wt + wT + a = wt + a + 2p;
|
T =  . (12.2)
. (12.2)
Это важная связь периода с циклической (круговой) частотой колебания.
Число колебаний в единицу времени называется просто частотой — n. Частота n измеряется в герцах [1 Гц = 1 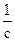 = 1 с–1] и является величиной, обратной периоду n =
= 1 с–1] и является величиной, обратной периоду n =  .
.
Любая система, в которой возможно гармоническое колебание, называется гармоническим осциллятором. Гармонические колебания могут происходить в системе в том случае, если она отвечает двум условиям:
1. Колебательная система должна обладать положением устойчивого равновесия;
2. При выходе из положения равновесия в системе должна возникать возвращающая сила, пропорциональная смещению.
Рассмотрим несколько примеров механических гармонических осцилляторов.