Собственные колебания физического маятника

Физическим маятником можно назвать любое твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной точки или оси. Возьмём в качестве такого маятника однородный тонкий стержень длиной l (рис. 12.7).

Рис. 12.7

Ось колебания проходит через точку О, отстоящую на расстоянии d от центра масс стержня — точки С. Запишем основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:

. (12.12)

Здесь — момент внешних сил, вращающих тело относительно горизонтальной оси x. Такая сила в системе одна — сила тяжести. Её момент равен произведению величины силы на «плечо» — на расстояние от оси вращения до линии действия силы — b:

,

где j — угол, который образует стержень с вертикалью.

 

 

Вычисляя момент инерции стержня I_x, воспользуемся теоремой Гюйгенса-Штейнера:

.

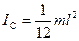— момент инерции стержня относительно оси, проходящей через точку центра масс.

Учитывая, что угловое ускорение 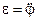. Запишем уравнение колебаний физического маятника в следующем виде:

.

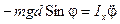В случае малых углов отклонения, когда Sinj » j, это уравнение можно упростить:

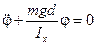. (12.13)

Уравнение (12.13) — дифференциальное уравнение колебаний физического маятника в стандартном виде. Известно, что решением подобного уравнения является гармоническая функция:

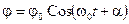, (12.14)

где частота собственных незатухающих колебаний:

. (12.15)

Период собственных колебаний физического маятника

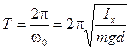. (12.16)

Сравнивая (12.16) с периодом колебаний математического маятника 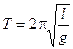, легко установить, что их периоды будут совпадать, если длина математического маятника окажется равной 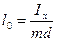, l₀ — называется приведенной длиной физического маятника, она равна длине такого математического маятника, период которого совпадает с периодом данного физического маятника.

Для вычисления частоты и периода собственных незатухающих колебаний, например, тонкого стержня, нужно в соответствующих формулах [(12.15), (12.16)] использовать момент инерции стержня 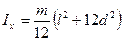.