Уравнение бегущей волны. Волновое уравнение

Уравнение бегущей волны выражает зависимость смещения колеблющейся частицы от координаты и времени.

Рассмотрим вывод уравнения плоской синусоидальной волны. Пусть упругая волна распространяется вдоль оси x. Если ξ(x,t)= Asinωt будет уравнением колебания точки (частицы), то такие же колебания частицы, отстоящей от источника на расстоянии x, произойдут позже, то есть с опозданием на время x/υ. Точка (частица) на расстоянии x будет иметь такое смещение в момент времени t , как и начальная точка в момент (t -x/υ). Тогда уравнение колебаний частиц, колеблющихся в плоскости XOY, или уравнение плоской бегущей волны будет:

 

ξ(x,t) = Asinω(t - x/υ). (6.1)

 

Если фазовая скорость имеет обратное направление (-υ), то есть волна распространяется в обратном направлении, то

 

ξ(x,t) = Asinω(t + x/υ). (6.2)

 

Без учета поглощения энергии в общем случае уравнение плоской синусоидальной волны, распространяющейся вдоль положительного направления оси OX, будет:

 

ξ(x,t) = Asin[ω(t ± x/υ) + φ₀],

где A - амплитуда волны,

φ₀- начальная фаза колебаний, определяемая выбором начала отсчета x и t ;

[ω(t ± x/υ) + φ₀] - фаза плоской волны.

Введем в уравнения (6.1) и (6.2) волновое число:

 

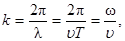(6.3)

где λ - длина волны;

T - период колебаний;

ω - циклическая частота.

Обобщив (6.1), (6.2) и (6.3), перепишем уравнение плоской бегущей волны в виде:

 

ξ(x,t) = Asin(ωt ± kx + φ₀), (6.4)

 

Направление волны зависит от знака (+) или (-) перед kx.. .

Аналогично можно показать, что уравнение сферической синусоидальной волны (её волновые поверхности имеют вид концентрических сфер) записывается так:

ξ(r,t) = 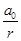sin(ωt ± kr + φ₀), (6.5)

где 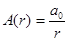- амплитуда волны,

a₀ - физическая величина, численно равная амплитуде на единичном расстоянии от центра волны.

Из (6.5) видно, что амплитуда колебаний сферической синусоидальной волны не остается постоянной, а убывает с расстоянием r от источника по закону 1/r .

 

 

Существуют и другие формы записи синусоидальной плоской и сферической волны1.

Уравнение волны (6.4) – одно из возможных решений общего дифференциального уравнения с частными производными, описывающее процесс распространения возмущения в среде. Такое уравнение называется волновым. Его можно получить продифференцировав (6.4) по два раза, сначала по t, а затем по x:

 

 

 

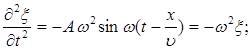
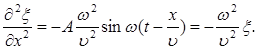
Сравнивая эти уравнения получим волновое уравнение для плоской волны, распространяющейся вдоль оси OX:

 

 

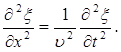
Волновое уравнение в общем случае:

 

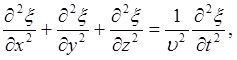
или

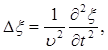
где

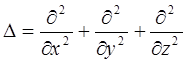- оператор Лапласа.