МЕХАНИКА

 

МЕХАНИКА,

МОЛЕКУЛЯРНАЯ ФИЗИКА

И ТЕРМОДИНАМИКА

Курс лекций по физике для студентов инженерно-технических специальностей

МЕХАНИКА

Лекция 1. Элементы кинематики

План лекции

1.1. Механика. Система отчета.

1.2. Перемещение и путь.

1.3. Скорость и ускорение.

1.4. Движение материальной точки по окружности.

Механика. Система отчета

· классическую механику, изучающую движение макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме; · релятивистскую механику, изучающую движение макроскопических и… · квантовую механику, изучающую движение микроскопических тел (отдельных атомов и элементарных частиц)

Перемещение и путь

Рассмотрим кинематику материальной точки. Существует два способа геометрического описания движения точки. Первый способ. С помощью радиус-вектора , являющегося функцией времени t,…

Рис. 1.2

Прямая, проведенная из точки, в которой началось движение, в точку, где находится материальная точкав определенный момент времени, называетсявектором перемещения.В общем случае векторперемещения не совпадает с траекторией, но при достаточно малом перемещениитраекторию можно заменить хордой. Длина траектории совпадает с длиной вектора перемещения и в случае прямолинейного движения.

Скорость и ускорение

 

Рис. 1.3

 

Среднюю скорость можно определить как

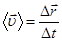(1.3)

В случае малого промежутка времени (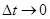), получаем выражение для мгновенной скорости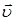

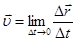(1.4)

Математически понятие мгновенной скорости совпадает с определением производной (или иначе: физический смысл понятия производной есть мгновенная скорость)

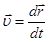(1.5)

Скорость–векторная величина, направление которой определяется касательной к траектории в данной точке. Для вектора скорости справедливо векторное сложение.

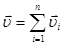(1.6)

Например, такое часто наблюдается в строительстве. Так, автомобильный кран, имеющий выдвижную стрелу, поднимает груз. При этом стрела, находясь под углом, выдвигается и еще вращается вокруг вертикальной оси. Груз участвует в трех движениях и обладает, соответственно, скоростями: вверх - 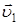, вдоль оси стрелы - 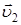и окружной скоростью 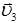. Результирующая скорость 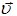будет:

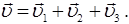
Часто на практике используется средняя скорость.

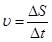– средняя скорость (1.7)

При достаточно малом промежутке времени 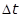имеем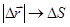

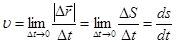– мгновенная скорость (1.8)

 

Физическая величина, характеризующая быстроту изменения скорости по величине и по направлению при неравномерном движении, называетсяускорением. Если за промежуток времени 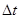скорость изменилась на 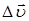, то

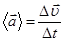–среднее ускорение (1.9)

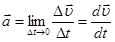– мгновенное ускорение (1.10)

Пусть материальная точка движется по криволинейной траектории со скоростью 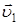, которая изменяется по величине и по направлению (рис. 1.4). За время 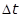точка переместилась из положения А в положение В и прошла путь 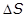, равный дуге АВ. За это время материальная точка приобрела скорость 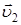. Переместив вектор 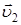в положение А, определим приращение скорости на пути АВ; оно будет равно .

 

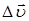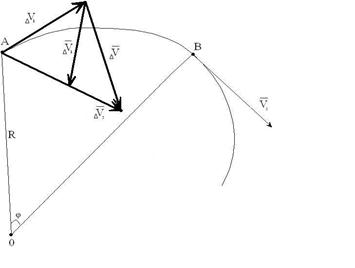
Рис. 1.4

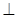
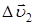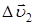Разложим на составляющие и , совпадающий с .

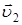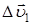– характеризует изменение скорости по направлению;

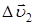– характеризует изменение скорости по величине:

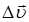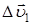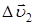=+ (1.11)

 

Ускорение будет равно

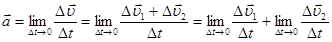(1.12)

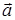– полное ускорение, состоящее из двух компонент.

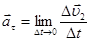– тангенциальное (или касательное) ускорение, характеризующее изменение скорости по модулю за время 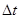. Это означает, что тангенциальное ускорение есть производная от скорости по времени.

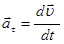(1.13)

Тангенциальное ускорение – векторная величина, направленная в сторону вектора скорости.

Определим составляющую .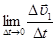

Эта составляющая характеризует изменение скорости по направлению и называется нормальным ускорением

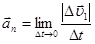(1.14)

При 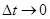точка А близка к точке В. В этом случае путь можно считать дугой окружности радиуса R. При этом дуга мало отличается от хорды АВ. Треугольники АОB и АСD подобны, как равнобедренные.

Отсюда следует, что

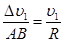(1.15)

При 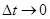, , 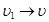но так как 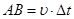, то

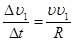(1.16)

и получаем

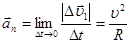(1.17)

Нормальное ускорение 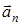также называют центростремительным ускорением. Оно направлено по нормали к касательной к центру кривизны траектории.

Полное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 1.5):

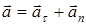(1.18)

При 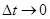имеем .

 

Рис. 1.5

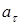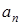В зависимости от и движение можно классифицировать следующим образом:

1. 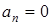, 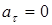– движение прямолинейное равномерное;

2. 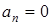, 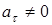– движение прямолинейное ускоренное;

3. 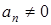, , 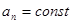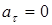– равномерное движение по окружности.

 

Движение по криволинейной траектории можно представить как прямолинейное движение и движение по окружностям разных радиусов (рис. 1.6)

 

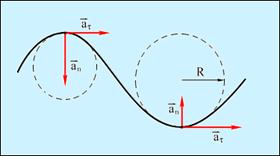
Рис. 1.6

Движение материальной точки по окружности

Рассмотрим движение точки по окружности радиуса R (рис. 1.7) Пусть через промежуток времени положение точки определяется углом поворота .   Рис. 1.7 -средняя угловая скорость

Рис. 1.8

При равномерном вращении ()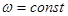

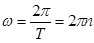
Τ – период вращения – время одного полного оборота точки,

n – частота вращения – количество оборотов в единицу времени;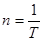

При неравномерном вращении ()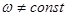

– среднее угловое ускорение

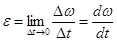– мгновенное угловое ускорение

Угловое ускорение – величина векторная 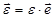, где 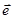– единичный вектор, совпадающий с направлением оси вращения.

Если 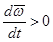, вектор углового ускорения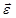совпадает с направлением вектора угловой скорости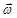– вращение равноускоренное;

Если 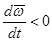, вектор углового ускорения 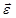направлен противоположно вектору угловой скорости 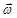– вращение равнозамедленное.

Размерность углового ускорения [e] = рад/с², ([e]= с^-2).

Установим связь между линейным и угловым ускорениями.

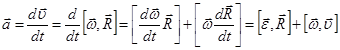
Так как 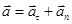, то , .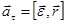

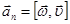Законы движения точки (тела) по окружности аналогичны законам поступательного движения. Уравнение вращательного движения можно вывести из уравнений поступательного движения, заменив путь S углом поворота φ, скорость u – угловой скоростью ω, ускорение а – угловым ускорением ε.

Например,

®

®

 

 

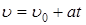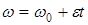
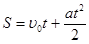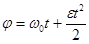
Лекция 2. Динамика материальной точки

План лекции

2.1. Первый закон Ньютона. Инерциальная система отсчета.

2.2. Масса. Импульс. Закон сохранения импульса.

2.3. Сила. Второй и третий законы Ньютона.

2.4. Сила трения.

2.5. Сила упругости.

2.6. Сила тяготения.

Первый закон Ньютона. Инерциальная система отсчета

В качестве I закона Ньютона принят закон инерции, открытый Галилеем, который формулируется следующим образом: если на материальное тело не действуют… Так как движение относительно и его характер зависит от выбора системы… Классическая механика постулирует, что существует системы отсчета, в которых все свободные тела движутся прямолинейно…

Масса. Импульс. Закон сохранения импульса

(2.1) Масса характеризует инерционные свойства тела, то есть является мерой… Для замкнутой системы, то есть для системы, где материальные точки взаимодействуют только друг с другом и не…

Сила. Второй и третий законы Ньютона

, (2.6) следовательно (2.7)

Сила трения

Различают трение внутреннее (жидкое или вязкое) и внешнее. Внутренним трением называется трение, возникающее между частями одного и того… (2.10)

Рис. 2.1

F_тр = μ₀ N (2.12)

где μ₀ – коэффициент трения покоя, N – сила нормального давления.

При движении одного тела по поверхности другого возникает трение скольжения.

F_тр = μ N (2.13)

μ – коэффициент трения скольжения

μ < μ₀, то есть сила трения покоя больше силы трения скольжения.

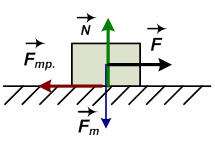
Для определения коэффициента трения используется наклонная плоскость (рис. 2.3). Угол наклонной плоскости увеличивают до тех пор, пока тело не начнет скатываться по плоскости. В этом случае сила трения 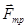будет равна сказывающей силе :

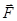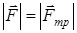, т.е. ,

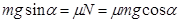Рис. 2.2.

откуда 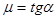(2.14)

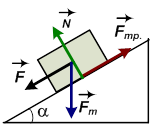
Рис. 2.3

Одним из видов внешнего трения является трение качения, которое проявляется, когда тело катится по опоре (рис.2.4). Оно значительно меньше трения скольжения m_k << m.

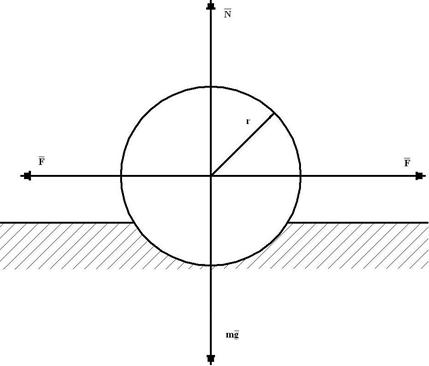
Рис. 2.4

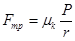(2.15)

где P – вес катка, r – радиус, μ_k – коэффициент трения качения.

Из (2.15) видно, что сила трения качения обратно пропорциональна радиусу катящегося тела.

Трение играет большую роль в природе и технике. В некоторых случаях трение играет положительную роль и его стремятся увеличить (например, изготовление автомобильных шин со специальным рисунком протектора, увеличивающим трение между колесами и поверхностью дорожного покрытия, посыпание песком дорог во время гололеда). Но иногда приходится бороться с негативными проявлениями, вызываемыми трением с помощью смазок. В данном случае используется тот факт, что внутреннее трение, возникающее между слоями жидкости значительно меньше внешнего трения, возникающего между частями твердых тел. Другой способ уменьшить внешнее трение – заменить трение скольжения трением качения, применяя шариковые и роликовые подшипники и т.д.

Сила упругости

Различают следующие виды деформации: всесторонние растяжение или сжатие, сдвиг, кручение. Рассмотрим однородный стержень длиной , диаметром d и площадью поперечного… (2.17)

Рис. 2.5

, – имеют разные знаки, так как при растяжении длина стержня увеличивается (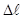>0), а диаметр уменьшается (∆d<0) и наоборот при сжатии.

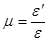(2.20)

где 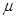– коэффициент Пуассона[1].

Английский ученый Р.Гук[2] экспериментально установил, что для малых деформаций напряжение 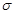прямо пропорционально относительному удлинению .

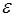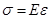(2.21)

где Е – модуль Юнга[3].

Если 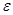=1 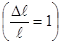, то Е = .

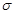Другими словами, модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице (т.е. ).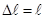

Модуль Юнга – теоретическая величина, так как нет материала (кроме резины) который мог бы удлиняться в 2 раза без разрыва.

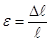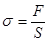Подставляя в формулу (2.21) и получим

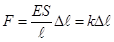(2.22)

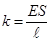– коэффициент упругости.

Закон Гука приобретает вид

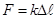(2.23)

Деформация подчиняется закону Гука до известного предела.

Из рис.2.6 видно, что линейная зависимость 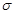(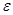) соответствует участку оa (деформация на этом участке – упругая); участок ab соответствует пластической деформации, а od – остаточной деформации. Значение 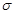при котором тело разрушается – называется пределом прочности. Если предел упругости совпадает с пределом прочности тело называется хрупким.

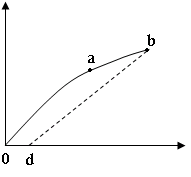Рис. 2.6

 

Сила тяготения

(2.24) где F – сила всемирного тяготения (или гравитационная сила); m1 и m2 массы… Коэффициент пропорциональности G – гравитационная постоянная, которая определяется опытным путем и равна…

Из формулы (2.27) видно, что

Если тело находится на высоте h (r=R+h) то (2.30) В результате действия силы тяготения (а также действия других сил) тело действует на опору или подвес с силой, которая…

Лекция 3. Динамика твердого тела

План лекции

3.1. Момент силы.

3.2. Основные уравнения вращательного движения. Момент инерции.

3.3. Кинетическая энергия вращения.

3.4. Момент импульса. Закон сохранения момента импульса.

3.5. Аналогия между поступательным и вращательным движением.

Момент силы

Рассмотрим движение твердого тела вокруг неподвижной оси. Пусть твердое тело имеет неподвижную ось вращения ОО (рис.3.1) и к нему приложена произвольная сила .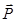

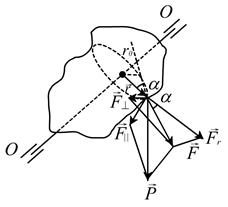
Рис. 3.1

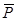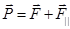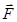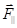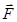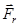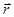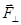Разложим силу на две составляющие силы , сила лежит в плоскости вращения, а сила – параллельна оси вращения. Затем силу разложим на две составляющие: – действующую вдоль радиус-вектора и – перпендикулярную ему.

Не любая сила, приложенная к телу, будет вращать его. Силы 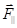и 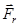создают давление на подшипники, но не вращают его.

Сила 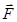может вывести тело из равновесия, а может – нет в зависимости от того, в каком месте радиус-вектора 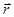она приложена. Поэтому вводится понятие момента силы относительно оси. Моментом силыотносительно оси вращения называется векторное произведение радиуса-вектора 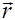на силу .

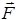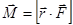(3.1)

Вектор 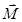направлен по оси вращения и определяется правилом векторного произведения или правилом правого винта, или правилом буравчика.

 

Модуль момента силы

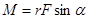(3.2)

где α – угол между векторам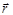и и .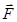

Из рис.3.1. видно, что _.

r₀ – кратчайшее расстояние от оси вращения до линии действия силы и называется плечом силы. Тогда момент силы можно записать

М = F r₀ . (3.3)

Из рис. 3.1.

,

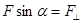где F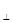– проекция вектора 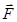на направление, перпендикулярное вектору радиус-вектору 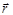. В этом случае момент силы равен

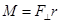. (3.4)

Если на тело действует несколько сил, то результирующий момент силы равен векторной сумме моментов отдельных сил, но так как все моменты направлены вдоль оси, то их можно заменить алгебраической суммой. Момент будет считаться положительным, если он вращает тело по часовой стрелке и отрицательным, если против часовой стрелки. При равенстве нулю всех моментов сил (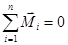), тело будет находиться в равновесии.

Понятие момента силы можно продемонстрировать с помощью «капризной катушки». Катушку с нитками тянут за свободный конец нитки (рис. 3.2).

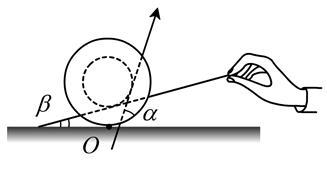
Рис. 3.2

В зависимости от направления силы натяжения нити 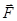катушка перекатывается в ту или иную сторону. Если тянуть под углом α, то момент силы относительно оси О (перпендикулярной к рисунку) вращает катушку против часовой стрелки и она откатывается назад. В случае натяжения под углом β вращающий момент направлен против часовой стрелки и катушка катится вперед.

Используя условие равновесия (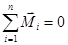), можно сконструировать простые механизмы, которые являются «преобразователями» силы, т.е. прикладывая меньшую силу можно поднимать и перемещать разного веса грузы. На этом принципе основаны рычаги, тачки, блоки разного рода, которые широко используются в строительстве. Для соблюдения условия равновесия в строительных подъемных кранах для компенсации момента силы, вызванного весом груза, всегда имеется система противовесов, создающая момент силы обратного знака.

 

Основное уравнение вращательного движения. Момент инерции

М = М1 + М2 + … +Мn (3.4) где М1= F1 r1, М2= F2 r2, …, Mn = Fn rn Согласно II закону Ньютона, каждая сила F, действующая на элемент массой Dm, вызывает ускорение данного элемента a,…

Рис. 3.3

Зная связь между линейным угловым ускорением ε (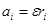) и что угловое ускорение для всех элементов одинаково, формула (3.6) будет иметь вид

М = 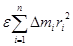(3.7)

где

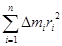=I (3.8)

I – момент инерции тела относительно неподвижной оси.

Тогда мы получим

М = I ε (3.9)

Или в векторном виде

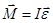(3.10)

Это уравнение является основным уравнением динамики вращательного движения. По форме оно сходно с уравнением II закона Ньютона. Из (3.10) момент инерции равен

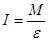(3.11)

Таким образом, моментом инерции данного тела называется отношение момента силы к вызываемому им угловому ускорении. Из (3.11) видно, что момент инерции является мерой инертности тела по отношению к вращательному движению. Момент инерции играет ту же роль, что и масса при поступательном движении. Единица измерения в СИ [I] = кг·м². Из формулы (3.7) следует, что момент инерции характеризует распределение масс частиц тела относительно оси вращения.

Итак, момент инерции элемента массы ∆m движущегося по окружности радиусом r равен

I = r²Dm (3.12)

Для тела содержащего n элементов

I= 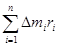(3.13)

В случае непрерывного распределения масс сумму можно заменить интегралом

I= ∫ r²dm (3.14)

где интегрирование производится по всей массе тела.

Отсюда видно, что момент инерции тела зависит от массы и её распределения относительно оси вращения. Это можно продемонстрировать на опыте (рис.3.4).

 

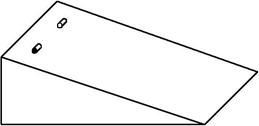
Рис. 3.4

 

Два круглых цилиндра, один полый (например, металлический), другой сплошной (деревянный) с одинаковыми длинами, радиусами и массами начинают одновременно скатываться. Полый цилиндр, обладающий большим моментом инерции, отстанет от сплошного.

Вычислить момент инерции можно, если известна масса m и ее распределение относительно оси вращения. Наиболее простой случай – кольцо, когда все элементы массы расположены одинаково от оси вращения (рис. 3.5):

 

I = 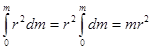(3.15)

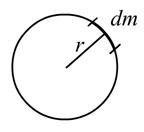
Рис. 3.5

Приведем выражения для моментов инерции разных симметричных тел массой m.

1.Момент инерции кольца, полого тонкостенного цилиндра относительно оси вращения совпадающей с осью симметрии.

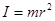, (3.16)

r – радиус кольца или цилиндра

2.Для сплошного цилиндра и диска момент инерции относительно оси симметрии

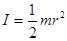(3.17)

3. Момент инерции шара относительно оси, проходящей через центр

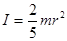(3.18)

r – радиус шара

4. Момент инерции тонкого стержня длинной l относительно оси, перпендикулярной стержню и проходящей через его середину

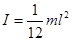(3.19)

l – длина стержня.

Если ось вращения не проходит через центр масс, то момент инерции тела относительно этой оси определяется теоремой Штейнера.

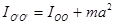(3.20)

Согласно этой теореме, момент инерции относительно произвольной оси О’O’ (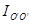) равен моменту инерции относительно параллельной оси, проходящей через центр масс тела (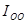) плюс произведение массы тела на квадрат расстояния а между осями (рис. 3.6).

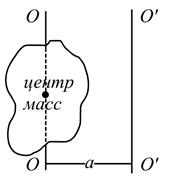
Рис. 3.6

Кинетическая энергия вращения

(3.21)

Рис. 3.7

Вспомним по (3.13), что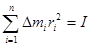– момент инерции относительно оси ОО.

Таким образом, кинетическая энергия вращающегося тела

Е_к = 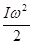(3.22)

Мы рассмотрели кинетическую энергию вращения вокруг неподвижной оси. Если тело участвует в двух движениях: в поступательном и вращательном движениях, то кинетическая энергия тела складывается из кинетической энергии поступательного движения и кинетической энергии вращения.

Например, шар массой m катится; центр масс шара движется поступательно со скоростью u (рис. 3.8).

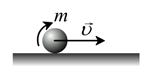
Рис. 3.8

Полная кинетическая энергия шара будет равна

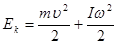(3.23)

3.4. Момент импульса. Закон сохранения
момента импульса

 

Физическая величина равная произведению момента инерции I на угловую скорость ω, называется моментом импульса (моментом количества движения) L относительно оси вращения.

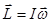(3.24)

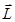– момент импульса величина векторная и по направлению совпадает с направлением угловой скорости .

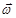Продифференцировав уравнение (3.24) по времени, получим

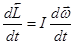или 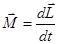(3.25)

где, М – суммарный момент внешних сил. В изолированной системе момент внешних сил отсутствует (М=0) и

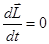, отсюда 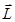= const (3.26)

Полученный результат представлен собой закон сохранения момента импульса (момента количества движения): момент импульса (момент количества движения) замкнутой системы является величиной постоянной.

При поступательном движении системы внутренние силы не могут изменить ни импульса системы, ни ее массы, поэтому скорость центра масс остается неизменной.

При вращательном движении внутренние силы могут изменить распределение масс, а значит, момент инерции относительно оси вращения. Следствием этого должно быть изменение угловой скорости вращения тела

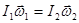(3.27)

Пример

1. Фигурист на коньках изменением положения рук, регулирует свой момент инерции, а, следовательно, и скорость вращения своего тела.

2. Спортсмен, когда делает сальто, поджимает к туловищу руки и ноги, чтобы уменьшить момент инерции и увеличить угловую скорость.

 

Аналогия между поступательным и вращательным движением

  Поступательное движение Вращательное движение Путь S Скорость Ускорение Масса m Сила F … Формальной заменой указанных величин в формулах поступательного движения можно… Например:

План лекции

4.1. Работа переменной силы. Мощность.

4.2. Энергия. Кинетическая и потенциальная энергии.

4.3. Закон сохранения энергии в механике.

Работа переменной силы. Мощность.

А = Fs · S (4.1) Эта формула справедлива для прямолинейного движения при Fs= const, а также… А = F · S cos (4.2)

Рис. 4.1.

На графике видно, что работа равна площади заштрихованного прямоугольника.

Если работа совершается под действием переменной силы, т.е. F ≠ const (F = F (S)), то графически работа будет равна площади под кривой (рис. 4.2).

 

Чтобы найти работу переменной силы разобьем пройденный путь на элементарные отрезки пути dS_i. Тогда работа на элементарном отрезке пути будет:

 

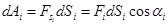(4.4)

Если при прямолинейном движении элементарный отрезок пути выбрать таким, чтобы F = const и 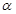= const, то на пути от S₁ до S₂ работа будет равна:

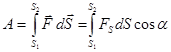(4.5)

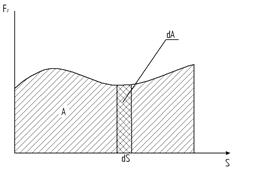
Рис. 4.2

Для характеристики быстроты совершения работы вводится понятие мощности. Мощность N – физическая величина, равная отношению работы ΔА к промежутку времени Δt, в течение которого она совершается

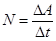(4.6)

Если тело движется со скоростью u под действием силы F, то мощность равна произведению проекции силы на перемещение на скорость тела

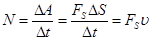(4.7)

Если мощность со временем изменяется, то вводится понятие мгновенной мощности

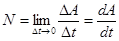(4.8)

 

Мощность измеряется в ваттах: 1Вт = 1Дж/с.

Энергия. Кинетическая и потенциальная энергии

В зависимости от вида движения различаются формы энергии: механическая, тепловая, электромагнитная, ядерная и др. Энергия может переходить из одной… В механике различают два вида энергии: кинетическую и потенциальную. Кинетическая энергия определяется работой, которая необходима, чтобы вызвать движение. Кинетическая энергия – эта…

Закон сохранения энергии в механике

Е = Ек + Еn (4.20) Чтобы вывести закон сохранения механической энергии рассмотрим замкнутую… Допустим, что система состоит из материальных точек m1, m2, …, mn, движущихся со скоростями u1, u2, …, un .

План лекции

5.1. Основные характеристики колебательного движения.

5.2. Кинетическая, потенциальная и полная энергии гармонических колебаний.

5.3. Уравнение гармонических колебаний. Маятники.

5.4. Затухание колебания.

5.5. Вынужденные колебания. Резонанс.

5.6. Явление резонанса в строительстве.

Основные характеристики колебательного движения

В данном курсе физики мы будем изучать два наиболее распространенных класса колебаний: механические и электрические. Среди разнообразных колебаний основную и существенную роль играют так… Рассмотрим гармонические колебания на примере колеблющейся точки.

Рис.5.1.

Если точку спроецировать на оси X и Y, то ее проекции будут совершать колебания и удовлетворяют следующим уравнениям соответственно

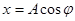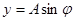, (5.1)

где, φ= ω₀t + φ₀ – фаза колебаний

Тогда

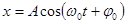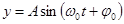и (5.2)

где х и y – смещения колеблющейся точки от положения равновесия;

А – амплитуда колебания (максимальное смещение);

φ₀ – начальная фаза (при t = 0);

ω₀ – круговая (циклическая) частота колебаний.

Точка совершает одно полное колебание за время Τ, называемое периодом колебания. Частота колебаний ν (число колебаний в единицу времени) есть 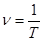. Между указанными величинами существует взаимосвязь

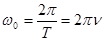(5.3)

Геометрический смысл параметров уравнений (5.2) можно объяснить с помощью векторных диаграмм. Выберем на оси Х точку О и из этой точки под углом φ₀ проведем вектор А. Будем вращать вектор А с угловой скоростью ω₀ и тогда его проекция на ось будет смещаться на величину x (рис. 5.2).

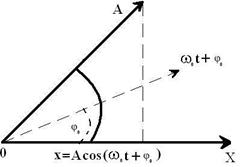
Рис.5.2.

Колеблющаяся точка обладает скоростью и ускорением. Скорость материальной точки

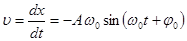(5.4)

Ускорение материальной точки

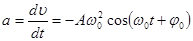(5.5)

С учетом формулы (5.2) получим

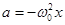(5.6)

Сравнивая уравнения (5.2), (5.4) и (5.5) замечаем, что скорость опережает смещение на π/2. Фазы ускорения и смещения различаются на π (изменяются в противофазе). Графические зависимости смещения, скорости и ускорения от времени показаны на рис.5.3.

Умножив обе части равенства уравнения (5.6) на массу m материальной точки, получим 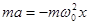(5.7)

Используя II закон Ньютона, получаем

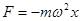(5.8)

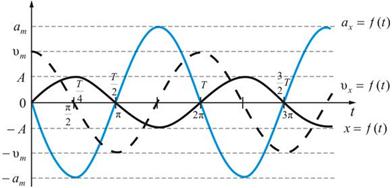
Рис.5.3.

Таким образом, чтобы совершались гармонические колебания на материальную точку должна действовать сила F, пропорциональная смещению x, которая возвращает ее в положение равновесия

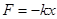(5.9)

где, k – некоторый коэффициент (зависящий от свойств колеблющейся системы) и называемой жесткостью.

Из уравнения (5.7) и (5.8) видно, что .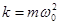

Кинетическая, потенциальная и полная энергии гармонических колебаний

Е = Ек + Еп (5.10) Кинетическую энергию можно найти, зная массу m и скорость u (5.11)

Уравнение гармонических колебаний. Маятники

ma = -kx (5.17) где, k – жесткость системы,; х – смещение; а – ускорение материальной точки. … Сделав соответствующие подстановки в (5.17), получим

Пружинный маятник

Груз массой m, подвешенный на упругой пружине представляет собой пружинный маятник (рис.5.4). Если груз оттянуть вниз и отпустить, то под действием силы F = -kx маятник будет совершать колебания; k – коэффициент жесткости (в данном случае коэффициент упругости).

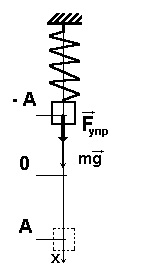
Рис.5.4.

Уравнение движения маятника имеет вид 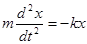или ,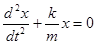

Его решением является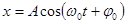

Это значит, что пружинный маятник совершает гармонические колебания с циклической частотой ω₀

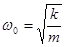, с другой стороны .

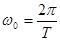Период колебаний пружинного маятника

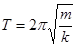(5.21).

Физический маятник

(5.22) где, I – момент инерции относительно оси О; l – плечо силы Fτ; при малых углах .

Рис.5.5.

Из (5.22) получаем дифференциальное уравнение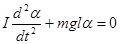

Или 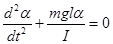(5.23)

Сравнив уравнение (5.23) с уравнением гармонического осциллятора (5.19), получим

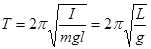, (5.24)

где, 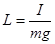– приведенная длина физического маятника.

От точки подвеса О на линии ОС на расстоянии L находится точка О₁, называемая центром качения. Точки О и О₁ обладает свойством взаимозаменяемости.

Математический маятник

Момент инерции материальной точки относительно оси вращения проходящей через точку подвеса равен Математический маятник является частным случаем физического маятника, поэтому, период колебаний математического…

Затухающие колебания

Движение в реальных системах всегда сопровождается трением и в результате потери энергии колебания затухают. Свободные колебания всегда являются затухающими. Затухающие колебания можно продемонстрировать с помощью установки изображенной на рис.5.6. Если привести в колебание воронку с песком, то при ее движении всыпающийся песок оставляет след затухающих колебаний.

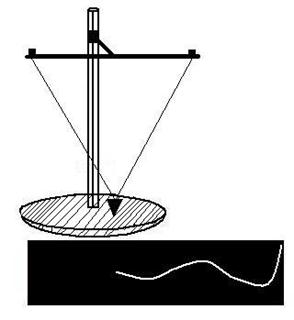
Рис.5.6

При малых скоростях колебания сила трения пропорциональна скорости

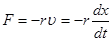(5.25)

где r – коэффициент сопротивления.

На колеблющуюся систему массой m действует сумма сил (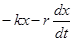), которая вызывает ускорение 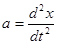этой системы, т.е.

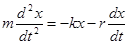
или

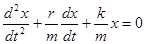(5.26)

Зная, что 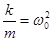и, обозначив 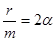(α – коэффициент затухания), получим дифференциальное уравнение затухающих колебаний

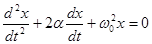(5.27)

Решением этого уравнения при условии ω₀ > α является выражение

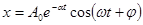(5.28)

Здесь 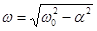– частота затухающих колебаний, а постоянные А₀ и φ зависят от начальных условий.

На рис.5.7. представлен график функции (5.28). На графике пунктиром показаны кривые затухания амплитуд. Уменьшение амплитуд происходит по закону

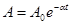(5.29)

где α – коэффициент затухания, характеризующий скорость затухания колебаний.

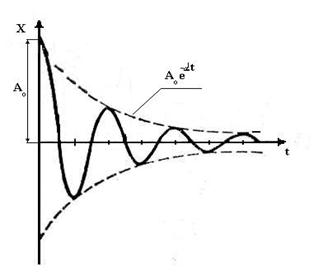
Рис.5.7

Найдем время τ, в течение которого амплитуда уменьшается в е раз. Если в формулу (5.29) подставить 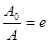, получим

at = 1 или .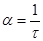

Следовательно, коэффициент затухания обратно пропорционален времени, за которое амплитуда уменьшается в е раз.

Мерой затухания является величина называемая логарифмическим декрементом затухания δ. Логарифмический декремент затухания есть логарифм отношения двух последовательных амплитуд колебаний отличающихся на период.

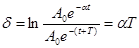(5.30)

При малых значениях δ пользуются понятием добротности .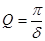

Период затухающих колебаний равен

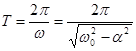
При 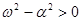система совершает периодические затухающие колебания, как показано на рис.5.8.

Когда 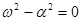, то Τ ® ∞. Это значит, что движение перестает быть периодическим (см. рис.5.8). В зависимости от начальных условий система возвращается в положение равновесия по одной из двух указанных кривых.

Вынужденные колебания. Резонанс

Колебания реальной системы всегда происходят с трением и с течением времени они затухают. Чтобы колебания были незатухающими, необходимо компенсировать потери энергии воздействием на систему внешней силой.

Рис.5.8

 

Наиболее простой случай, когда внешняя сила F изменяется по гармоническому закону

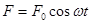(5.31)

где F₀ – амплитудное значение силы,

ω – циклическая частота действия вынуждающей силы.

Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными.

К силам, действующим при свободных колебаниях (5.26), прибавляется вынуждающая сила

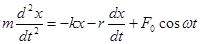
или

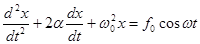(5.32)

где 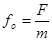,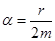– коэффициент затухания;

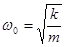– собственная циклическая частота колебаний системы.

Это неоднородное дифференциальное уравнение незатухающих колебаний, решение которого равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

Установившиеся вынужденные колебания происходят по гармоническому закону с частотой, равной частоте внешней силы ω. В этом случае решением уравнения (5.32) будет

(5.33)

где, А – амплитуда, φ – сдвиг фаз между смещением и вынуждающей силой.

А и φ зависят от соотношений между ω и ω₀. Чтобы установить эти зависимости воспользуемся уравнением (5.33) и подставим в уравнение (5.32) значение х, , .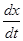

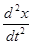После соответствующих преобразований получим:

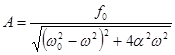(5.34)

и 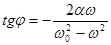(5.35)

Из выражения (5.34) видно, что амплитуда А зависит от частоты вынуждающей силы ω и при 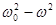она максимальна. Резкое возрастания амплитуды вынужденных колебаний, когда циклические частоты вынуждающей силы и свободных колебаний близки друг к другу называется резонансом, а соответствующая частота – резонансной частотой. Резонансные кривые изображены на рис.5.9.

Из уравнения (5.34) видно, что при ω = 0

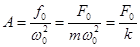
при ω ≈ ω₀ (при резонансе)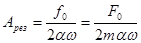

 

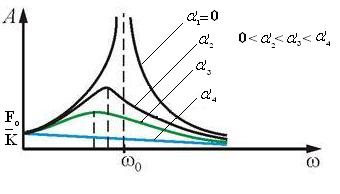
Рис.5.9

Из формулы (5.35) следует, что при ω = 0 φ = 0 фазы силы и колебания совпадают, а при резонансе (ω ≈ ω₀, φ = π/2) сила опережает колебания на π/2. При увеличении ω сдвиг фаз увеличивается и при ω >> ω₀, φ → π. Это значит, что фаза колебаний почти противоположна фазе вынуждающей силе.

В подтверждение сказанному можно продемонстрировать явление резонанса и сдвиг фаз на установке (рис.5.10). Если тяжелый правый маятник вывести из равновесия, то крайний левый, одинаковый по длине маятник, придет в резонанс и будет максимально отклоняться. При этом их колебания по фазе будут отличаться на π/2.

 

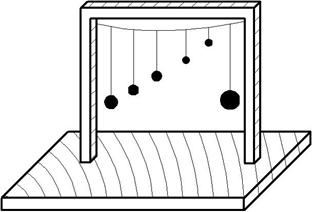
Рис.5.10

Явление резонанса может быть вредным и полезным. Явление резонанса учитывается в строительстве, используется в акустике, радиотехнике и т.д.

Сложение гармонических колебаний одного направления

Рассмотрим два случая: сложение гармонических колебаний, направленных по одной прямой и происходящих во взаимно перпендикулярных направлениях.   А) Сложим гармонические колебания, происходящие по одной прямой с одинаковой частотой

Рис.5.12

Метод биений широко используется на практике. Этот метод используется для определения частоты тона для настройки музыкальных инструментов, анализа слуха и т.д.

Сложение взаимно перпендикулярных колебаний

(5.46) Для определения уравнения траектории результирующего движения, необходимо из… (5.47)

Рис.5.13 Рис.5.14

Иными словами, при значениях φ₂ – φ₁ = kπ. (k = 0, 1, 2, …) в уравнение (5.50) 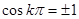, 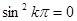и мы получаем уравнение прямой .

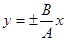3) При 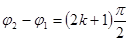уравнение траектории будет представлять собой эллипс

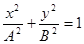
При равенстве амплитуд А + В = R эллипс превращается в окружность

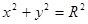
При сложении взаимно перпендикулярных колебаний разных, но кратных между собой частот (например, 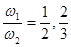и т.д.), получаются различные траектории материальной точки, называемые фигурами Лиссажу (рис.5.15).

Рис.5.15

Вид фигур зависит от соотношения частот ω₁/ω₂ и разности начальных фаз (φ₂ – φ₁) слагаемых колебаний.

Исследования частот и разности фаз складываемых колебаний с помощью фигур Лиссажу широко используется на практике, особенно в измерительной технике.

 

Лекция 6. Механические волновые процессы

План лекции

6.1. Возникновение волны. Продольные и поперечные волны.

6.2. Уравнение бегущей волны. Волновое уравнение.

6.3. Фазовая и групповая скорости.

6.4. Волны в упругих средах.

6.5. Звук и его характеристики.

6.6. Элементы акустики и их значение в строительстве.

6.7. Использование энергии упругих волн в строительстве.

Возникновение волны. Продольные и поперечные волны

Если в среде колеблется частица, то она приводит в колебание соседние частицы. Процесс распространения колебаний называется волной. Направление…   Поверхность, до которой дошли колебания частиц к моменту времени t, называется фронтом волны. Совокупность точек…

Уравнение бегущей волны. Волновое уравнение

Рассмотрим вывод уравнения плоской синусоидальной волны. Пусть упругая волна распространяется вдоль оси x. Если ξ(x,t)= Asinωt будет…   ξ(x,t) = Asinω(t - x/υ). (6.1)

Фазовая и групповая скорости

Рассмотрим простой случай, когда волновой пакет состоит из двух волн, распространяющихся вдоль оси OX с близкими частотами ω и ω +… Тогда  

Волны в упругих средах

  Рассмотрим распространение механической волны в круглом стержне диаметром D,… Δl = υ Δt. (6.10)

Звук и его характеристики

Характеристикой звука является интенсивность I, мерой которой служит энергия W , переносимая ежесекундно сквозь единицу поверхности S…    

Лекция 7. Элементы теории относительности

План лекции

7.1. Принцип относительности Галилея.

7.2. Постулаты специальной теории относительности. Замедление времени.

7.3. Преобразования Лоренца для координат и времени.

7.4. Следствия из преобразований Лоренца.

7.5. Релятивистская динамика. Связь массы и энергии.

 

Принцип относительности Галилея

Рис.7.1  

Постулаты специальной теории относительности.

Специальная теория относительности (СТО) представляет собой современную теорию… В СТО, как и в классической механике, предполагается, что время однородно (не зависит от выбора начала отсчета),…

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Лекция 8. Молекулярно-кинетическая теория газа

План лекции

8.1. Молекулярно-кинетический и термодинамический методы.

8.2. Термодинамические параметры.

8.3. Основные уравнения молекулярно-кинетической теории газа.

8.4. Средняя кинетическая энергия молекул. Распределение молекул по степеням свободы.

8.5. Скорости молекул. Распределение молекул по скоростям.

Молекулярно-кинетический и термодинамический методы

– молекулярно-кинетический (молекулярно-статистический); – термодинамический. Молекулярно-кинетический метод исходит из того, что все тела состоят из молекул и атомов, которые находятся в…

Термодинамические параметры

При изучение свойств вещества термодинамическим методом используют понятие термодинамической системы, под которой понимается совокупность… Состояние системы характеризуется физическими величинами, называемые… Рассмотрим термодинамическую систему, представляющую собой газ массой m. Вследствие непрерывного хаотического движения…

Основное уравнение молекулярно-кинетической теории газа

Столкновение молекул идеального газа со стенкой сосуда носит характер упругого соударения. Это значит, что молекулы при столкновении со стенкой… (8.12) где, Δр – изменение импульса, m0 – масса одной молекулы

Средняя кинетическая энергия молекул. Распределение молекул по степеням свободы

Количество независимых величин, с помощью которых определяется положение системы в пространстве называетсячислом степеней свободы. Если средняя кинетическая энергия поступательного движения равна , то нетрудно… где i – суммарное количество поступательных, вращательных и колебательных степеней свободы.

Скорости молекул. Распределение молекул по скоростям

Средняя кинетическая энергия ‹ε0› поступательного движения молекулы массой m0, с одной стороны равна (8.19) С другой стороны, эта энергия может быть определена через температуру

Рис.8.2.

Из графика видно, что наибольшая площадь находится под максимумом кривой. Следовательно, наиболее вероятная скорость близка к скорости большинства молекул.

Из закона распределения (8.24) можно найти среднюю арифметическую скорость ‹u› поступательного движения молекул идеального газа

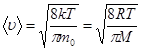(8.26)

Все представленные скорости молекул характеризуют состояние идеального газа и близки друг к другу, т.е. их соотношение: ‹u_в›:‹u_кв›:‹u› = 1:1,1:1,2.

 

 

Лекция 9. Газ во внешнем поле.
Молекулярные столкновения и явления переноса

План лекции

9.1. Идеальный газ во внешнем поле.

9.2. Число соударений между молекулами и средняя длина свободного пробега молекул.

9.3. Явления переноса. Коэффициент переноса. Ультраразреженные газы

 

Идеальный газ во внешнем поле

Возьмем две площадки единичной площади, расположенных на расстоянии dx; на эти площадки будет оказываться давление, которое равно соответственно Р и…

Рис.9.1

Разность давлений dP равняется суммарной силе, действующей на частицы в объеме Sdx (S =1 м³), т.е.

dP = nFdx (9.1)

где, n – объемная плотность молекул;

F – сила, действующая на одну молекулу с координатой х.

Сила F связана с потенциальной энергией Е_п

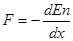(9.2)

После подстановки (9.2) в (9.1) получим

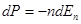(9.3)

Для идеального газа Р = nkТ. Предполагая, что Τ = соnst

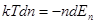(9.4)

Проинтегрировав обе части равенства (9.4) получаем

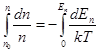(9.5)

учитывая, что n₀ – объемная плотность молекул в точке где Е_n = 0, получим

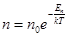(9.6)

Полученная формула устанавливает связь изменения объемной плотности газа с потенциальной энергией его молекул и называется формулой Больцмана.

Если (9.6) умножить на kТ, получим уравнение для расчета давления

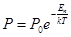(9.7)

В поле тяжести Земли на высоте h молекула массой m₀ обладает потенциальной энергией Е_п= m₀gh

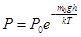(9.8)

Уравнение (9.8) называется барометрической формулой.

Подставив вместо 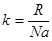и m₀Na = M, получим для барометрической формулы:

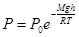(9.9)

График зависимости давления газа от высоты Р( h) представлен на рис.9.2.

Рис.9.2

Чем больше молекулярная масса, тем быстрее давление убывает с высотой. Поэтому с увеличением высоты атмосфера обогащается легкими парами.

Число соударений между молекулами и средняя длина свободного пробега молекул

Соответственно, количество столкновений Z равно (9.10) где, n – количество молекул в единице объема, концентрация молекул.

Рис.9.4

Эффективный диаметр зависит от скорости сталкивающихся молекул, т.е. от температуры газа.

Явления переноса. Коэффициент переноса. Ультраразреженные газы

- теплопроводности или переноса энергии; - диффузии или переноса массы; - внутреннего трения или переноса импульса (количества движения).

Рис.9.5

Дальнейшая откачка (понижение давления) влечет за собой убывание коэффициента теплопроводности, что используется в термосах, в современных электронных приборах.

Лекция 10. Первое начало термодинамики и

Его применение

План лекции

10.1. Первое начало термодинамики. Внутренняя энергия газа. Работа газа.

10.2. Теплоемкости газов

10.3. Работа газа при изопроцессах.

10.4. Адиабатический процесс

 

Первое начало термодинамики

dQ = dU + dA (10.1) Полученное уравнение носит название уравнения Клаузиуса[8]. В более корректной… dQ = dU + dA, (10.2)

Теплоемкости газов

, (10.11) Молярной теплоемкостью Сm называют количество теплоты, необходимое для… , (10.12)

Рис.10.3

Классическая теория теплоемкости недостаточна для объяснения C_V(T) в широком диапазоне температур. Объяснение такого поведения теплоемкости дает квантовая механика.

 

Работа газа при изопроцессах

В термодинамике работа расширения газа от объема V1 до V2 вычисляется по формуле (10.10) Напомним, что I-е начало термодинамики может быть записано как

Адиабатический процесс

Если dQ = 0, то из уравнения (10.22) следует, что dA = –dU где dA = PdV, , или .

Рис.10.4

 

При адиабатическом процессе работа совершается за счет изменения внутреннейэнергии (см. (10.1)).Для одного моляdA = -C_mVdT или после интегрирования

A = -C_mV (T₂ – T₁) = C_mV T₁(1 – T₂/ T₁) . (10.33)

 

Преобразуя выражение (10.32) в виде

T₂/ T₁ = (V₁/V₂)^γ

и используя выражение для C_mV в виде

C_mV = C_mV R/R = C_mV R/ (C_mp - C_mV) = R/(γ – 1), (10.34)

получим

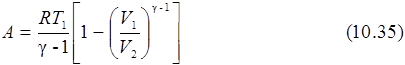
Для любой массы газа m:

 

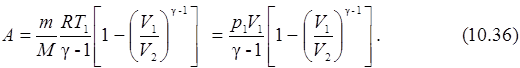
Адиабатический - это быстропротекающий процесс. Например, процесс, происходящий в двигателях внутреннего сгорания можно считать адиабатическим. Адиабатические процессы применяются и в строительной технике, например, в различных строительных пистолетах, в краскораспылителях и т. д.

 

 

Лекция 11. Второе начало термодинамики

План лекции

11.1. Круговые процессы (циклы).

11.2. Цикл Карно и его кпд для идеального газа.

11.3. Второе начало термодинамики.

11.4. Приведенное количество теплоты. Энтропия.

Круговые процессы (циклы)

Обратимым процессом называется такой процесс, который может протекать как в прямом, так и в обратном направлениях. Если при прямом ходе на каком-то… Важное значение в термодинамике имеют так называемые круговые (или замкнутые)… График цикла представляет собой замкнутую линию. На рис.11.1 изображен прямой цикл. Он соответствует тепловой машине,…

Рис.11.1

В этом цикле при сообщении теплоты газу, он расширяется (dV > 0) и совершает положительную[11] работу А₁, которая численно равна площади под кривой 1а2. В процессе 2б1 газ сжимается (dV < 0) и совершает отрицательную работу А₂, численно равную площади под кривой2б1.

Алгебраическое суммирование работ (А = А₁ + А₂) дает в целом положительную работу, совершаемую газом за цикл. Эта работа численно равна площади замкнутой кривой 1а2б1.

Применим к круговым процессам первое начало термодинамики. Для процесса 1а2 оно будет иметь вид

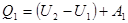(11.1)

где Q₁ – теплота, передаваемая газу от нагревателя; U₁ и U₂ – внутренняя энергия газа в точках 1 и 2; А₁ – работа, совершаемая газом.

При сжатии газ совершает работу А₂ и отдает тепло Q₂, что равнозначно получению -Q₂. Для процесса 2б1 уравнение первого начала термодинамики имеет вид

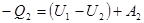(11.2)

При сложении уравнений (11.1) и (11.2), получим

Q₁ – Q₂ = A₁ + A₂ или Q₁ – Q₂ = A (11.3)

где А = A₁ + A₂.

При сообщении системе теплоты Q₁ только часть ее превращается в работу А, а часть Q₂ передается холодильнику. Поэтому термический коэффициент полезного действия h для кругового процесса равен

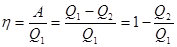(11.4)

Цикл называется обратным, если за цикл совершается отрицательная работа. Такой процесс протекает в направлении как показано на рис. 11.2.

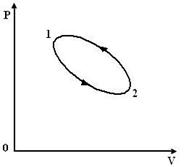
Рис.11.2

Обратный цикл соответствует работе холодильной машины, т.е. такой системе, которая отбирает теплоту от холодильника и передает нагревателю за счет работы внешних сил.

Цикл Карно и его к.п.д. для идеального газа

Французский инженер Сади Карно[12], работая над повышением к.п.д. тепловых машин, пришел к выводу, что газ совершает наиболее экономичный цикл, когда он состоит из двух изотерм и двух адиабат.

Цикл Карно для идеального газа представлен на рис. 11.3.

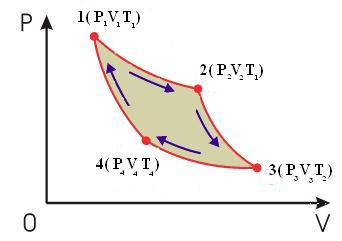
Рис.11.3

Из состояния 1 газ, получив от нагревателя Q₁, расширяется изотермически (Т₁ = const) и переходит в состояние 2. Из состояния 2 газ переводится в состояние 3 адиабатически. Здесь работа расширения происходит за счет убыли внутренней энергии, поэтому температура падает до Т₂. Переходя из состояния 3 в состояние 4 газ изотермически сжимается, отдавая холодильнику количество теплоты Q₂. При переходе из состояния 4 газ адиабатически сжимается до первоначального состояния 1.

Подсчитаем к.п.д. для описанного цикла Карно.

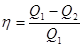(11.4)

При изотермическом расширении газа на участке 1-2 работа совершается за счет Q₁

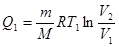(11.5)

На участке 3-4

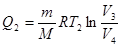(11.6)

Подставив (11.5) и (11.6) в (11.4), получим

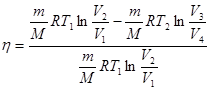(11.7)

Можно доказать, что

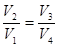(11.8)

Запишем уравнения адиабаты для адиабатических процессов на участках 2-3 и 4-1

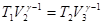и 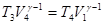(11.9)

Из уравнений (10.9) нетрудно получить уравнение (11.8). Следовательно, в уравнении (11.7) 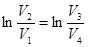. После соответствующих сокращений, к.п.д. цикла Карно выразим, используя значения температуры нагревателя Т₁ и холодильника Т₂.

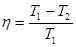(11.10)

Отсюда видно, что термический к.п.д. цикла Карно не зависит от природы газа (рабочего тела) и является только функцией температур нагревателя и холодильника. Это утверждение носит название теоремы Карно.

Термический к.п.д. цикла Карно равен к.п.д. кругового процесса для обратимого и больше для необратимого цикла, т.е.

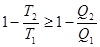(11.11)

Второе начало термодинамики

Из (11.4) видно, что h = 1, если Q2 = 0, т.е. тепловая машина могла бы превращать все тепло, полученное от нагревателя в работу, ничего не отдавая… Формулировка Клаузиуса II начала термодинамики – теплота сама собой не может… Формулировка Томсона II начала термодинамики – невозможен вечный двигатель второго рода, т.е. такой периодический…

Приведенное количество теплоты. Энтропия

(11.12) Отсюда или (11.13) Учитывая, что теплота Q2 отрицательна, выражение (11.13) примет вид

Лекция 12. Реальные газы

План лекции

12.1. Уравнение Ван-дер-Ваальса.

12.2. Изотермы Ван-дер-Ваальса и их анализ.

12.3. Внутренняя энергия реального газа. Эффект Джоуля-Томсона.

Уравнение Ван-дер-Ваальса

(12.1) где Р – давление, V0 – объем одного моля газа, Т – температура, R – молярная… При выводе этой формулы мы пренебрегали объемом молекул и их взаимодействием. Для реального газа при увеличении…

Рис.12.1

Сила притяжения между молекулами, а, следовательно, и добавочное давление P_i прямо пропорционально концентрации газа n₀ как справа, так и слева, т.е. P_i ~ n₀ × n₀. (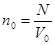, где N – количество молекул). Тогда

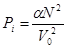(12.3)

Обозначим αN² через постоянную а, характеризующую силы молекулярного притяжения и перепишем уравнение Ван-дер-Ваальса (12.2) для одного моля газа в виде

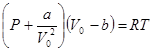(12.4)

Для массы газа m уравнение примет вид

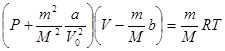(12.5)

где M – молярная масса; V – объем газа; a – поправка на объем b – поправка на силы притяжения.

Изотермы Ван-дер-Ваальса и их анализ

(12.6) При постоянной температуре Т уравнение (12.6) устанавливает связь между… Кривые P = f(V) при разных значениях Т называются изотермами Ван-дер-Ваальса. На рис. 12.2 показана одна из таких…

Рис. 12.2

Выясним физический смысл различных участков изотерм Ван-дер-Ваальса. Участки 7-6 и 2-1 имеют нормальный характер, т.е. давление возрастает при уменьшении объема.

Участок 5-3 соответствует неестественному поведению газа, когда его сжатие приводит к уменьшению давления.

Участки 6-5 и 3-2 отвечают метастабильным состояниям переохлажденного пара и перегретой жидкости.

Реальная экспериментальная изотерма отличается от теоретической тем, что участок 6-2 соответствует прямой линии, параллельной оси V. С повышением температуры эта прямая уменьшается и стягивается в точку К, называемую критической. Этой точке соответствуют критические параметры (Р_K, V_K, T_K). Критические параметры можно связать с поправками а и b, входящими в уравнение Ван-дер-Ваальса. При Т = Т_К и Р = Р_К уравнение (12.6) примет вид

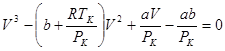(12.7)

и все три корня будут одинаковы и равны критическому объему V_K. В этом случае (12.7) тождественно уравнению

(12.8)

Значит коэффициенты при одинаковых степенях V в уравнениях (12.7) и (12.8) равны

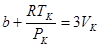
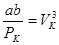
Отсюда

.

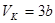
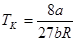Экспериментальные изотермы при разных температурах показаны на рис.12.3.

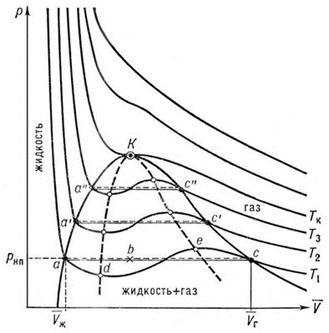
Рис.12.3.

Точка К точкой перегиба критической изотермы, выше которой находятся монотонные изотермы. Если соединить между собой точки начала и конца прямолинейных отрезков изотерм, то на диаграмме P и V получим кривую фазового равновесия жидкости и пара. За этой кривой под критической изотермой справа – область, соответствующая пару, слева – жидкости.

Область над критической соответствует газообразному состоянию. Пар отличается от газообразного состояния тем, что он при сжатии превращается в жидкость. Газ же при температуре, выше критической ни под каким давлением не может быть сжижен. Так целый ряд газов (O₂, N₂, H₂, He₂) не поддавался сжижению. Д.И.Менделеев объяснил все эти неудачи тем, что сжижение производилось при температуре больше критической.

Внутренняя энергия реального газа. Эффект Джоуля-Томсона

Тогда работа, затрачиваемая на преодоление сил притяжения пойдет на увеличение потенциальной энергии межмолекулярного взаимодействия dEn, т.е. (12.10) Откуда .