Принцип относительности Галилея
Рассмотрим инерциальные системы координат К (х,у,z) и К’ (х’,у’,z’) . Пусть система К’ движется относительно системы К с постоянной скоростью υ0. Для простоты будем считать параллельными оси координат К и К’ (x||x’, y||y’, z||z’ - рис.7.1).
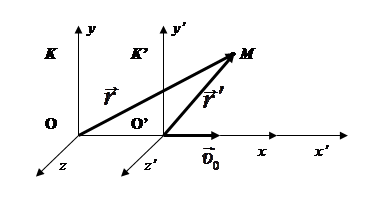
Рис.7.1
В момент времени t = 0 начало координат О’ совпадает с О.
В момент времени t точка М определяется радиус-вектором  относительно системы К и
относительно системы К и 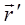 относительно К’. Из рисунка 7.1 видно, что
относительно К’. Из рисунка 7.1 видно, что
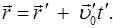 (7.1)
(7.1)
При этом t = t’ .
Запишем соотношение (7.1) в проекциях на оси координат:
 . (7.2)
. (7.2)
Уравнения (7.1) и (7.2), выражающие координаты движущейся точки в неподвижной системе К через координаты подвижной системы К’ называются преобразованиями Галилея.
Продифференцируем (7.1) по времени t и получим уравнение
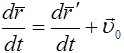
или
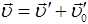 , (7.3)
, (7.3)
которое представляет собой закон сложения скоростей в классической механике.
Так как 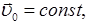
при дифференцировании (7.3) по времени t получим
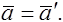 (7.4)
(7.4)
Таким образом, ускорения в обеих системах отсчета одинаковы, т.е. ускорение инвариантноотносительно преобразований Галилея.
Также
F = ma
инвариантно относительно преобразований Галилея, т.е.

Обобщая сказанное, можно сформулировать механический принцип относительности: уравнения механики Ньютона инвариантны относительно преобразований Галилея.