Малые колебания
Рассмотрим механическую систему , положение которой может быть определено с помощъю одной величины, например х. В этом случае говорят, что система имеет одну степень свободы.Величиной х может быть угол, расстояние, энергия, скорость, ускорение и т.п. Потенциальная енергия системы тогда будет функцией одной переменной х, т.е., 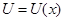 .Допустим что система обладает устойчивым положением равновесия. В этом положении тогда можно положить, что
.Допустим что система обладает устойчивым положением равновесия. В этом положении тогда можно положить, что 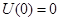 .
.
Разложим функцию 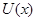 в ряд Маклорена (частный случай ряда Тейлора) по степеням х и ограничимся малыми колебаниями, т.е., степенями 2-го порядка. Энергию их отсчитываем от положения равновесия. Тогда:
в ряд Маклорена (частный случай ряда Тейлора) по степеням х и ограничимся малыми колебаниями, т.е., степенями 2-го порядка. Энергию их отсчитываем от положения равновесия. Тогда:
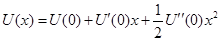
Производная 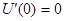 , а
, а 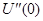 положительна для минимума функции. Обозначив
положительна для минимума функции. Обозначив 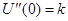 ,
, 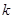 -константа, при этом
-константа, при этом 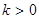 , получим:
, получим:
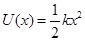 , это выражение аналогично энергии сжатой пружины.
, это выражение аналогично энергии сжатой пружины.
Используя связь между силой и потенциальной энергией: 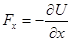 , найдем силу, действующую на систему:
, найдем силу, действующую на систему:
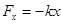 ,
,
что тождественно упругой силе деформации пружины. (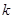 -не только коэффициент упругости, а и постоянная в разложении)
-не только коэффициент упругости, а и постоянная в разложении)
Поэтому силы вида 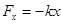 называют квазиупругими. Они направлены к положению равновесия, пропорциональны х, и называются возвращающими.
называют квазиупругими. Они направлены к положению равновесия, пропорциональны х, и называются возвращающими.
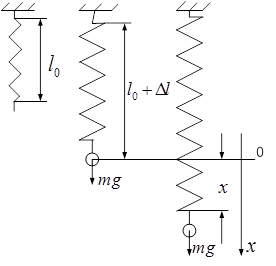
Рис.7,1
Пример гармонических колебаний: В положении равновесия 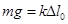 (*).Сместив шарик в положение х, получим удлинение
(*).Сместив шарик в положение х, получим удлинение 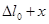 , а сила
, а сила 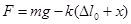 или с учётом (*)
или с учётом (*) 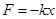 , т.е. результирующая сил тяжести и упругой является квазиупругая сила.
, т.е. результирующая сил тяжести и упругой является квазиупругая сила.
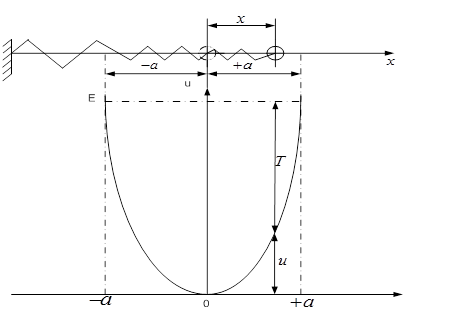
Рис.7,2
Дадим смещение 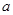 и отпустим шарик.Он будет двигаться к положению равновесия со скоростъю
и отпустим шарик.Он будет двигаться к положению равновесия со скоростъю 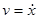 . Потенциальная энергия будет убывать, зато появится кинетическая
. Потенциальная энергия будет убывать, зато появится кинетическая 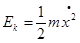 . Затем движение замедляется и шарик остановится, когда
. Затем движение замедляется и шарик остановится, когда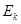 превратится в потенциальную энергию и смещение станет равным
превратится в потенциальную энергию и смещение станет равным 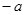 . Затем движение повторится в обратном направлении.
. Затем движение повторится в обратном направлении.