Уравнение плоской и сферической волн.
Уравнение волны выражает зависимость смещения колеблющейся частицы от ее кординат 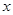 ,
,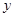 ,
,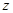 и времени
и времени  :
:  .
.
Эта функция должна быть периодической относительно времени, т.к. она описывает колебания частицы с координатами 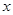 ,
,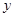 ,
,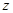 , и периодическая относительно координат, т.к. точки среды, отстоящие друг от друга
, и периодическая относительно координат, т.к. точки среды, отстоящие друг от друга
на длину волны 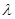 , колеблются одинаковым образом.
, колеблются одинаковым образом.
Найдём вид функции  для плоской волны, для гармонических колебаний, распространяющихся вдоль оси
для плоской волны, для гармонических колебаний, распространяющихся вдоль оси 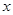 .Волновые поверхности здесь перпендикулярны оси
.Волновые поверхности здесь перпендикулярны оси 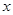 , и смещение
, и смещение  будет зависить только от
будет зависить только от 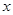 и
и  . Уравнение колебаний точек в плоскости
. Уравнение колебаний точек в плоскости  имеет вид:
имеет вид:
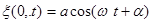
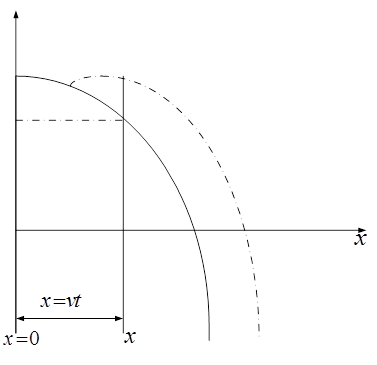
Рис.8,2
Найдем уравнение колебания для точки с произвольным 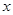 , дойти до которой волне требуется время
, дойти до которой волне требуется время  . Значит колебания частиц в плоскости
. Значит колебания частиц в плоскости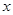 будут отставать во времени на
будут отставать во времени на 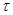 от колебаний в плоскости
от колебаний в плоскости  :
:
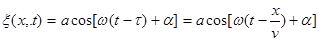
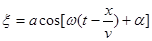 * - уравнение плоской волны, распространяющейся в направлении оси
* - уравнение плоской волны, распространяющейся в направлении оси 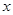 со скоростъю
со скоростъю  ,
,
величина  - фаза волны, начальная фаза
- фаза волны, начальная фаза 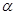 определяется выбором начала отсчёта
определяется выбором начала отсчёта 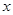 и
и  , для одной волны обычно принимают
, для одной волны обычно принимают 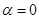 .
.
Зафиксировав определенное значение фазы 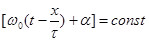 , можно найти связь между коорлинатой и временем для которых
, можно найти связь между коорлинатой и временем для которых  , а величина
, а величина 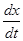 при этом даёт значение скорости, с которой перемещяется это значение фазы т.е., можно проследить движение определенной фазы волны. Взяв дифференциал от
при этом даёт значение скорости, с которой перемещяется это значение фазы т.е., можно проследить движение определенной фазы волны. Взяв дифференциал от  , получим:
, получим: 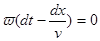 и
и  .
.
Таким образом, скорость распространения волны в уравнении (*) есть скорость перемещения фазы, поэтому ее называют фазовой скоростъю волны.
Уравнение (*) описывает волны, распространяющиеся в сторону возрастания 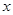 . Волна обратная имеет вид:
. Волна обратная имеет вид:  .
.
Уравнению волны можно придать более симметричный вид относительно 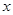 и
и  , если ввести понятие волнового числа
, если ввести понятие волнового числа
 и волнового вектора
и волнового вектора 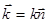 , где
, где 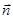 - нормаль к волновому фронту. Умножив числитель и знаменатель
- нормаль к волновому фронту. Умножив числитель и знаменатель 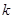 на
на 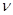 , получим:
, получим:  . Тогда,
. Тогда, 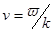 и уравнение волны:
и уравнение волны:
 .
.
Теперь найдем уравнение сферической волны для точечного источника. Все точки сферической волновой поверхности волны в однородной и изотропной среде будут колебаться с одинаковой фазой. Если фаза источника  , то фаза точек волновой поверхности радиуса
, то фаза точек волновой поверхности радиуса 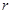 равна
равна  . Амплитуда колебаний сферической волны будет убывающей, даже если нет затухания и убывает по закону
. Амплитуда колебаний сферической волны будет убывающей, даже если нет затухания и убывает по закону  . Тогда уравнение сферической волны:
. Тогда уравнение сферической волны:  . Для поглощающей среды появится дополнительный множитель
. Для поглощающей среды появится дополнительный множитель  .
.
Уравнение плоской волны, распространяющейся в произвольном направлении 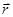 имеет вид:
имеет вид:  .
.