Перемещение, элементарное перемещение.
Пусть точка М движется от А к В по криволинейному пути АВ. В начальный момент ее радиус-вектор равен 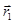 , а в момент времени
, а в момент времени 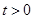 ее радиус-вектор равен
ее радиус-вектор равен  . Длина траектории точки -
. Длина траектории точки - .
.
Вектором перемещения точки за промежуток от  до
до 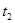 называется приращение радиуса-вектора
называется приращение радиуса-вектора 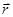 точки за это время
точки за это время  . Он направлен вдоль хорды стягивающий соответствующий участок траектории точки. Поэтому во всех случаях, кроме движения точки по прямой, модуль перемещения меньше длины пути за этот же
. Он направлен вдоль хорды стягивающий соответствующий участок траектории точки. Поэтому во всех случаях, кроме движения точки по прямой, модуль перемещения меньше длины пути за этот же 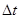 .
.
Однако, по мере уменьшения длины пути разность между хордой и перемещением уменьшается. Следовательно, рассматривая элементарное перемещение 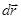 по траектории за достаточно малый промежуток времени
по траектории за достаточно малый промежуток времени 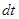 (от
(от  до
до 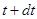 ), можно пренебречь отличием между
), можно пренебречь отличием между 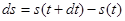 и модулем перемещения
и модулем перемещения  за это время. Значит, вектор
за это время. Значит, вектор 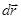 направлен по касательной к траектории в сторону движения точки, также как единичный вектор касательной
направлен по касательной к траектории в сторону движения точки, также как единичный вектор касательной 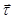 . Таким образом,
. Таким образом,

Вектор перемещения материальной точки за любой конечный промежуток времени от  до
до 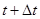 можно представить в виде:
можно представить в виде:
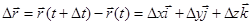 ,
,
где  приращения соответствующих координат точки за время
приращения соответствующих координат точки за время 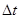 .
.
Следует заметить, что в математике и физике имеется некоторое различие в толковании смысла обозначений 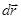 и
и  . В математике
. В математике 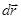 и
и  представляют собой дифференциалы соответствующих функций, т.е. равны линейным частям приращений этих функций при произвольном изменении аргумента от
представляют собой дифференциалы соответствующих функций, т.е. равны линейным частям приращений этих функций при произвольном изменении аргумента от  до
до 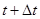 , рис. . По определению в математике дифференциал аргумента:
, рис. . По определению в математике дифференциал аргумента: 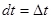 , а – функции:
, а – функции: 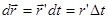 и
и  ;
;
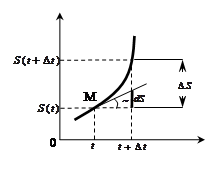

где  и
и  - производные по времени от функций
- производные по времени от функций 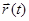 и
и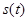 . Очевидно, что приращения функций
. Очевидно, что приращения функций 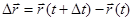 и
и 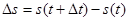 существенно отличаются от дифференциалов этих функций,что видно из рис..
существенно отличаются от дифференциалов этих функций,что видно из рис..
В физике различают произвольное (конечное) приращение аргумента 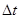 и дифференциал аргумента
и дифференциал аргумента 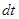 . Под дифференциалом аргумента
. Под дифференциалом аргумента 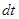 понимают столь малое его приращение (элементарное), при котором разностью между соответствующим приращением функции
понимают столь малое его приращение (элементарное), при котором разностью между соответствующим приращением функции 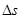 и линейной частью её приращения
и линейной частью её приращения  можно пренебречь т.е.
можно пренебречь т.е. 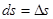 . Поэтому, в физике, используя предложенные Лейбницем обозначения производной
. Поэтому, в физике, используя предложенные Лейбницем обозначения производной 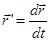
 , трактуют эти выражения как отношения не математических дифференциалов функции и аргумента, а малых (элементарных) приращений функции и аргумента.
, трактуют эти выражения как отношения не математических дифференциалов функции и аргумента, а малых (элементарных) приращений функции и аргумента.
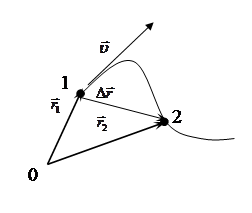 1.6. Скорость.
1.6. Скорость.
Для характеристики направления и быстроты движения точки вводится векторная физическая величина-скорость.
Пусть за произвольное время 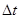 точка переместилась из т.1 в т.2. Вектор перемещения
точка переместилась из т.1 в т.2. Вектор перемещения  представляет собой приращение радиуса-вектора
представляет собой приращение радиуса-вектора 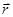 за время
за время 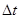
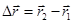 . Отношение
. Отношение 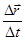 называется средней скоростью точки
называется средней скоростью точки 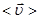 за время
за время 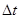 или скоростью перемещения. Направление вектора
или скоростью перемещения. Направление вектора 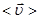 совпадает с перемещением
совпадает с перемещением  .
.
Скорость  точки в заданный момент времени, т.е., мгновенная скорость, определяется как предел отношения
точки в заданный момент времени, т.е., мгновенная скорость, определяется как предел отношения 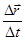 при
при 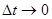 ,
,
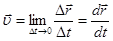
т.е. равна производной от радиуса-вектора 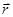 по времени и направлена по касательной к траектории в заданной точке в сторону ее движения. Модуль скорости
по времени и направлена по касательной к траектории в заданной точке в сторону ее движения. Модуль скорости  . Вектор
. Вектор  можно разложить по базису
можно разложить по базису  , т.е., на три составляющие по осям декартовой системы координат
, т.е., на три составляющие по осям декартовой системы координат
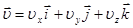 ;
;
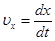 ;
;  ;
;  ;
;
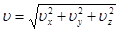 ;
;