Произведение массы материальной точки на ее ускорение равно действующей на нее силе.

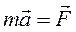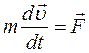или (1.1)

Уравнение (1.1) называют уравнением движения материальной точки. На всякую материальную точку зачастую действует несколько сил, поэтому в уравнении (1.1) под силой следует понимать результирующую (равнодействующую) силу:

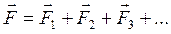
Уравнение движения можно представить и в следующем виде:

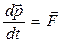(1.2)

где 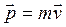- импульс материальной точки.

Во всех случаях, когда в опыте участвуют только два тела А и В и тело А сообщает ускорение телу В, обнаруживается, что и тело В сообщает ускорение телу А. Следовательно, действия тел друг на друга имеют характер взаимодействия. Ньютон постулировал данное свойство тел – третий закон:

силы, с которыми две материальные точки действуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки:

(1.3)

Уравнение (1.3) показывает, что силы взаимодействия всегда появляются парами, приложены к разным телам и являются силами одной природы.

Чтобы свести нахождение закона движения частицы к чисто математической задаче, необходимо, прежде всего – в соответствии с уравнением (1.1) - знать действующую на частицу силу, т.е. зависимость силы от определяющих ее величин. Наиболее фундаментальные силы, лежащие в основе всех механических явлений, - это силы гравитационные и электрические. Приведем выражения для этих сил в самом простом виде, когда взаимодействующие массы покоятся или движутся с малой (нерелятивистской) скоростью.

Сила гравитационного притяжения, действующая между двумя материальными точками, в соответствии с законом всемирного тяготения пропорциональна произведению масс точек m₁ и m₂, обратно пропорциональна квадрату расстояния r между ними и направлена по прямой, соединяющей эти точки:

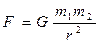где G = 6,67*10^-11 Н*м²/кг² – гравитационная постоянная.

Однородная сила тяжести:

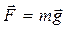где m – масса тела, g – ускорение свободного падения.

Вес тела – сила, с которой тело действует на опору (или подвес). Если опора (или подвес) неподвижна относительно данного тела, то вес совпадает с силой тяжести. В противном случае вес:

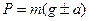где а – ускорение тела (с опорой) относительно Земли.

Упругая сила – сила, пропорциональная смещению материальной точки из положения равновесия и направленная к положению равновесия:

где 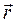– радиус-вектор, характеризующий смещение материальной точки из положения равновесия,

k – положительный коэффициент, зависящий от «упругих» свойств той или иной конкретной силы. Примером такой силы является сила упругой деформации при растяжении (сжатии) пружины или стержня – закон Гука:

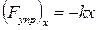где х – величина упругой деформации.

Сила трения скольжения, возникающая при скольжении данного тела по поверхности другого тела,

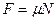где μ – коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей,

N – сила нормального давления, прижимающая трущиеся поверхности друг к другу. Сила трения направлена в сторону, противоположную направлению движения данного тела относительно другого.

Сила сопротивления, действующая на тело при его поступательном движении в газе или жидкости. Эта сила зависит от скорости тела относительно среды, причем направлена противоположно вектору скорости:

где α – положительный коэффициент, характерный для данного тела и данной среды.

Решение основного уравнения динамики материальной точки (1.1) есть основная задача динамики материальной точки. При этом возможны две противоположные постановки задачи.

1 Найти действующую на точку силу F, если известны масса m точки и зависимость от времени ее радиуса-вектора (t).

2 Найти закон движения точки, т.е. зависимость от времени ее радиуса-вектора 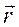(t), если известны масса m точки, действующая на нее сила 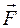(или 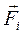) и начальные условия – скорость 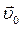и положение 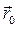точки в начальный момент времени.

В первом случае задача сводится к дифференцированию 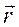(t) по времени, во втором – к интегрированию уравнения (1.1). В зависимости от характера и постановки конкретной задачи решение уравнения (1.1) проводят или в векторной форме, или в координатах, или в проекциях на касательную и нормаль к траектории в данной точке. Например, в проекциях на оси декартовых координат:

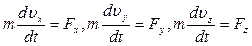(1.4)

Рассмотрим на конкретном примере алгоритм решения задач с помощью уравнений (1.4).

Задача. Небольшой брусок массы скользит вниз по наклонной плоскости, составляющей угол 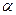с горизонтом. Коэффициент трения равен 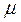. Найти ускорение бруска относительно плоскости (эта система отсчета предполагается инерциальной).

а) Изображение сил, действующих на брусок: сила тяжести 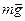, нормальная сила реакции 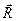со стороны плоскости и сила трения 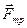(рисунок 1.1), направленная в сторону, противоположную движению бруска.

б) Выбор и связь бруска на плоскости с системой координат 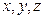, причем рационален выбор одной из осей по направлению движения.

в) Запись основного уравнения динамики в проекциях на выбранные оси:

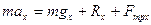где 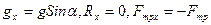. Поэтому

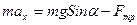Рисунок 1.1 Так как брусок движется только вдоль оси х, то это значит, согласно второму закону Ньютона, что сумма проекций всех сил на любое перпендикулярное оси х направление равна нулю. Здесь

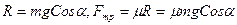г) В результате искомая величина
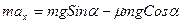