Сложение скоростей.

Рассмотрим точку М, совершающую сложное движение. Пусть эта точка, двигаясь вдоль своей относительной траектории АВ, совершает за промежуток времени 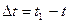относительное перемещение, определяемое вектором .

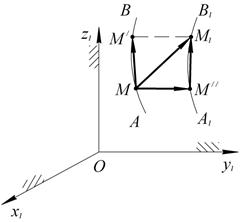
Рис. 2.14

Сама кривая АВ, двигаясь вместе с подвижными осями (О, х, y, z) (на рисунке не показаны), перейдет за тот же промежуток времени в какое-то новое положение А₁, В₁.

Одновременно та же точка кривой АВ, с которой в момент времени 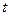совпадает точка М, совершит переносное перемещение, 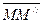. В результате этих движений точка М придет в положение М₁ и совершит за время 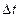абсолютное перемещение .

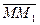Из векторного треугольника ММ^//М₁

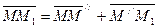
Деля обе части на 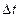и переходя к пределу получим:

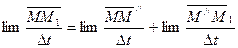
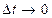
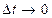
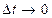
По определению:

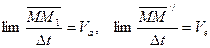
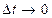
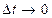
Что касается последнего соотношения, то так как при 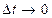кривая А₁В₁ стремится к совпадению с кривой АВ, то в пределе будем иметь

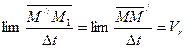
В результате находим, что

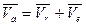(24)

То мы доказали следующую теорему о сложении скоростей: при сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.

Направлены векторы по касательным к соответствующим траекториям (рис.2.15).

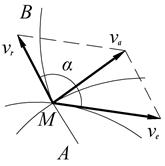
Рис. 2.15

 

Модуль абсолютной скорости:

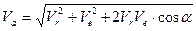
С помощью параллелограмма скоростей решается ряд задач кинематики точки:

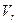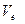– зная и можно найти абсолютную скорость,

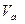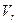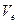– зная и направления скоростей и , можно найти модули этих скоростей,

– зная скорость 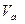и 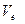можно найти скорость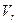

.
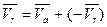